一级结构工程师结构力学考点讲义：第四节_第5页

　　七、位移法的基本原理

　　(一)位移法基本体系

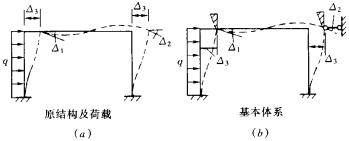
　　在结构的结点角位移和独立的结点线位移处增设控制转角和线位移的附加约束，使结 构的各杆成为互不相关的单杆体系，称为原结构的位移法基本结构。位移法基本结构在各 结点位移、外荷载(有时还有温度变化、支座位移等)作用下的体系称为位移法基本体系。图4—8a所示刚架的基本体系如图4—8b所示。

　　(二)位移法典型方程及其意义

　　为了使基本体系与原结构的受力情况相同，可以根据基本结构在给定荷载、温度变化、支座位移和各基本未知节点位移共同作用下，各附加约束中的总约束力等于零的条件建立位移法典型方程。对于有n个未知量的结构，位移法典型方程为

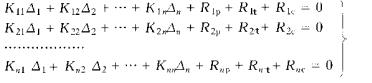
　　式中 Δi为结点位移未知量(i=1、2、…、n);Kij为基本结构仅由于Δj=1(j=1、2、…、n)在附加约束i中产生的约束力，为基本结构的刚度系数;Rip、Rit、Ric分别为基本结构仅由荷载、温度变化、支座位移作用，在附加约束i中产生的约束力，为位移法典型方程的自由项。

　　位移法典型方程(4—11)表示静力平衡方程。其中第一个方程表示基本结构在n个未知结点位移、荷载、温度变化、支座位移等共同作用下，第一个附加约束中的约束力等于零;第二个方程表示基本结构在n个未知结点位移、荷载、温度变化、支座位移等共同作用下，第二个附加约束中的约束力等于零。其余各式的意义可按此类推。

　　各未知结点位移的大小和方向必须受位移法典型方程的约束，各结点位移与平衡条件 是一一对应的，故满足位移法典型方程的各未知结点位移的解是唯一真实的解。

　　(三)系数和自由项的计算

　　位移法典型方程中的系数和自由项都是附加约束中的反力，它们都可按上述各自的定 义，利用各杆的刚度系数、固端弯矩、固端剪力由平衡条件求出。对于基本结构由支座位 移引起的固端力，也可由杆件的刚度系数求得。

　　位移法典型方程中的系数Kii称为主系数，它们恒为正值;Kij(i≠j)称为副系数，它们可为正值、负值、也可为零，根据反力互等定律，有Kij=Kji;各自由项的值可为正值、负值，也可为零。

　　(四)计算结构的最后内力

　　由位移法典型方程求出各未知节点位移Δi后，便可由叠加原理计算结构的最后内力：

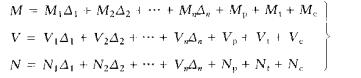
　　式中 Mi、Vi、Ni分别为Δi=1引起的基本结构的弯矩、剪力、轴力;Mp、Mt、Mc、Vp、Vt、Vc、Np、Nt、Nc、分别为基本结构由荷载、温度变化、支座位移引起的弯矩、剪力、轴力。

　　对梁和刚架，通常是先根据式(4—12)中的第一式求出各杆端弯矩，再用直杆弯矩图的叠加法作出各杆弯矩图，然后根据弯矩图由静力平衡条件求出各杆端剪力和轴力，并据此作出剪力图和轴力图。

　　在位移法的具体计算方法方面，除了上述基本体系与典型方程法外，还可直接通过建 立结点和截面的平衡方程，得到位移法基本方程。

　　位移法不仅可以计算超静定结构的内力，也可以计算静定结构的内力。