一级结构工程师结构力学考点讲义：第四节_第4页

　　五、等截面直杆的转角位移方程(刚度方程)

　　位移法是以杆件的转角位移方程作为计算基础的。转角位移方程表示杆件两端的杆端 力与杆端位移之间的关系式。

　　(一)平面桁架杆件

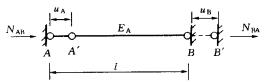
　　(图4—5)

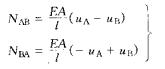
　　式中u、N分别表示杆端的轴向位移和轴向力，沿杆轴方向自A向B时为正。式(4—7)称为拉、压杆的刚度方程。

　　(二)两端固定的平面等截面直杆(图4—6a)

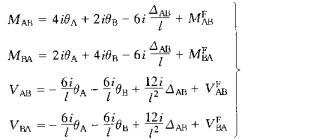
　　式中 i = EI/l称为线刚度。杆端截面转角θA、θB、弦转角β = ΔAB/l，杆端弯矩MAB、MBA，固端弯矩MABF、MBAF均以顺时针向转动为正。杆端剪力QAB、QBA，固端剪力QABF、QBAF均以绕隔离体顺时针向转动为正。图4—6所示杆端位移、杆端弯矩、杆端剪力的方向均为正号。

　　(三)一端固定另一端铰支的平面等截面直杆(图4-6b)

　　(四)一端固定另一端定向(滑动)支座的平面等截面直杆(图4-6c)

　　式(4—9)、(4—10)中各符号的意义及正、负号规定均与式(4—8)相同。式(4—8)、(4—9)、(4—10)称为前述各相应杆件的转角位移方程，式中含有θA、θB、ΔAB的各项分别代表该项杆端位移引起的杆端弯矩和杆端剪力，其前面的系数称为杆件的刚度系数，它们只与杆件的长度l、支座形式和抗弯刚度EI有关，又称为形常数。而固端弯矩、固端剪力则为仅由荷载产生的杆端弯矩、杆端剪力，它们均与荷载有关。

　　六、位移法的基本未知量

　　位移法以结构的刚结点的角位移和独立的结点线位移为基本未知量。角位移数等于刚性结点的数目。确定刚架独立的结点线位移数时，如果杆件的弯曲变形是微小的，且忽略受弯直杆的轴向变形，则刚架独立的结点线位移数就是刚架铰结图的自由度数(即运动的独立几何参数)。所谓刚架的铰结图就是将刚架的刚结点(包括固定支座)都改成铰结点后所形成的体系。如图4—7a所示刚架的结点角位移未知数等于7，在刚架铰结图的结点1、2、3处增设三根支杆后成为几何不变(图4—7b)，即该铰结图的自由度为3，故刚架的全部结点位移未知数等于10。

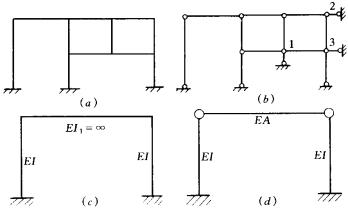
　　图4-7

　　如果考虑杆件的轴向变形，则平面结构每个结点的独立线位移未知数为2。如图 4—7a所示刚架的结点独立线位移未知数为2×7=14。

　　图4—7c所示刚架，其横梁不能弯曲，当不考虑各杆轴向变形时，两个刚结点不能转动，只有一个独立的结点线位移未知量。图4—7d所示结构，如果考虑柱顶轴力杆的轴向变形，而不计受弯杆柱子的轴向变形，则有两个独立的结点线位移未知量。