
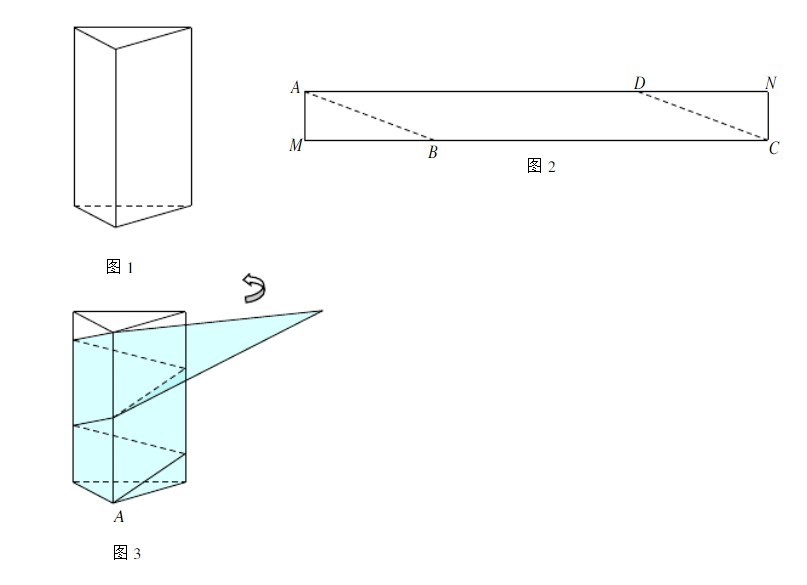
如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个 侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如 图2),然后用这条平行四边形纸带按如图 3 的方式把这个三棱柱包装盒的侧面进行包贴 (要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满。
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度。
参考答案:
(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30 ∵纸带宽为15,∴sin∠DAB=sin∠ABM=151302AMAB,∴∠DAB=30°.
(2)在图3中,将三棱柱沿过点A的侧棱剪开,得到如图甲的侧面展开图,将图甲种的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图乙中的平行四边形ABCD, 此平行四边形即为图2中的平行四边形ABCD 由题意得,知:BC=BE+CE=2CE=2×403cos30CD,∴所需矩形纸带的长为MB+BC=30·cos30°+403=553cm.
 ,我们将会及时处理。
,我们将会及时处理。