三、化简与求值(每小题4分，共12分)
21、(1)2 
(2) 
(- 
+ 
- 
(3)当x= 
时，求代数式 
的值
22、已知一次函数y=3x―2k的图像与反比例函数 
的图像相交，其中一个交点的纵坐标为6，求一次函数的图像与x轴、y轴的交点坐标(本题5分)
23、如图：已知一次函数y1=mx+n与反比例函数y2= 
的图象相交于A、B两点，AD⊥X 轴,利用图中的条件
(1)求出两函数的解析式
(2)求△AOB的面积
(3) 根据图象写出一次函数y1的值大于反比例函数y2的值的x的取值范围。(本题6分)
24、阅读下列材料后回答问题：
在平面直角坐标系中，已知x轴上两点A(x1,0)，B(x2,0)的距离记作AB=x2-x1.
如A(x1,y1)，B(x2,y2)是平面上任意两点，我们可以通过构造直角三角形来求A，B间距离.如图所示，过A，B分别向x轴，y轴作垂线AM1， AN1和BM2，BN2，垂足分别是M1(x1,0)，N1(0，y1)，M2(x2,0)，N2(0,y2)，直线AN1与NM2交于Q.
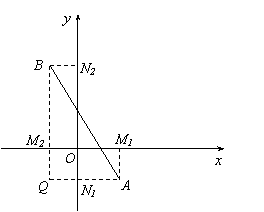
在Rt△ABQ中，AB2=AQ2+QB2.
∵AQ=M1M2=x2-x1
QB=N1N2=y2-y1
∴AB2=x2-x12+y2-y12
由此得任意两点A(x1,y1)，B(x2,y2)间距离公式AB=
. 如果某圆的圆心为O(0,0)，半径为r，设P(x,y)是圆上任一点，根据“圆上各点到定点(圆心)的距离都等于定长(半径)”.我们得到PO=r，即 
，整理得 
.我们称此式为圆心在原点，半径为r的圆的方程.
(1)写出圆心在原点，半径为5的圆的方程;
(2)如圆心在点P(2,3)，半径为3，求此圆的方程;
(3)方程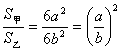
是否是圆的方程，如是，求出圆心坐标与半径. (本题6分)
。设S甲、S乙分别表示这两个正方体的表面积，则 
，又设V甲、V乙分别表示这两个正方体的体积，则 
。
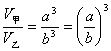(1)下列几何体中，一定属于相似体的是 ( )
A、两个球体 B、两个圆锥体 C、两个圆柱体 D、两个长方体
(2)请归纳出相似体的三条主要性质：①相似体的一切对应线段(或弧)长的比等于_______;②相似体表面积的比等于_______;③相似体体积的比等于_______。
(3)假定在完全正常发育的条件下，不同时期的同一人的人体是相似体，一个小朋友上幼儿园时身高为1.1米，体重为18千克，到了初二时，身高为1.65米，问他的体重是多少?(不考虑不同时期人体平均密度的变化)(本题6分)
26、某市为了缓解用电高峰期电力供不应求的矛盾，对居民生活用电采用两种计费方式，居民可自愿选取其中一种方式用电.(本题7分)
方式一：安装“分时”电表，使用“峰谷”电.分时用电分为高峰和低谷两个时段，每日8时至21时电价为0.55元/千瓦时(即“峰电”价)，21时至次日8时电价为0.30元/千瓦时(即“谷电”价).
方式二：使用原电表，电价与原来相同(不分时段)，为0.52元/千瓦时.
陈勇家从3月份开始使用“峰谷”电，已知他家3月份使用“峰电”和“谷电”共240千瓦时，其中使用“谷电”x千瓦时.
(1)请你写出陈勇家3月份的电费y(元)与“谷电”用电量x(千瓦时)的函数关式，并写出自变量x的取值范围;
(2)陈勇家3月份用多少千瓦时的“谷电”时，用“峰谷”电所需电费较少?
(3)经测算，3月份陈勇家的电费比使用原付费方式节约了19.8元，问：3月份他家用了多少千瓦时的“谷电”?
27、如图,已知:正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点B在函数
(k>0,x>0)的图象上,点P(m,n)是函数 (k>0,x>0)的图象上的任意一点,过点P分别作x轴、y轴的垂线,垂足分别是E、F.设矩形OEPF和正方形OABC不重合部分的面积为S. (本题8分)
(1)求B点坐标和k的值;(2)当S= 
时,求点P的坐标.
(3)写出S关于m的函数关系式
，我们将会及时处理。
