2020中考数学精选试题（5）

　　1.某养鱼户去年在鱼塘中投放了一批鱼苗，现在为了解这批鱼的平均重量，从中捞取10条鱼，测得其重量如下(单位：kg)

　　1.2　1.1　0.9　0.8　　l.3　　1.2　1.3　1.0　1.0　1.2

　　试估计这批鱼的平均重量约是 ▲ kg.

　　【答案】1.1。

　　【考点】平均数，用样本估计总体。

　　【分析】根据平均数的求法，捞取的10条鱼的平均数为：

　　(1.2+1.1+0.9+0.8+l.3+1.2+1.3+1.0+1.0+1.2)÷10=1.1(kg)。

　　根据用样本估计总体的方法，估计这批鱼的平均重量约是1.1 kg。

　　2.下图是由8块相同的等腰直角三角形黑白瓷砖镶嵌而成的正方形地面示意图，一只蚂蚁在上面自由爬动,并随机停留在某块瓷砖上,蚂蚁停留在黑色瓷砖上的概率是 ▲ .

　　【答案】1/2。

　　【考点】几何概率，等腰直角三角形的性质。

　　【分析】根据概率的求法，找准两点：①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率。因此，由于8块相同的等腰直角三角形中黑白瓷砖各4块，从而蚂蚁停留在黑色瓷砖上的概率是1/2。

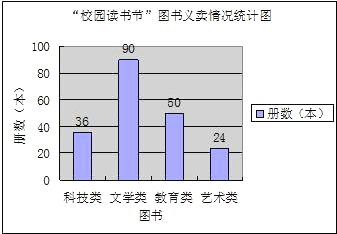
　　3.在“校园读书节”期间，学生会组织了一次图书义卖活动，提供了四种类别的图书，下图是本次义卖情况统计图，则这次活动共卖出的文学类图书本数占所有卖出本数的百分比是 　 ▲ 。

　　【答案】45%。

　　【考点】条形统计图，频数、频率和总量的关系。

　　【分析】从图中发现：本次活动共卖出的文学类图书本数是90本，所有卖出

　　总本数36+90+50+24=200，据此即可求得百分比：90÷(36+90+50+24)=45%。

　　4.布袋中装有2个红球，3个白球，5个黑球，它们除颜色外均相同，则从袋中

　　任意摸出一个球是白球的概率是　　▲　　.

　　【答案】3/10。

　　【考点】概率。

　　【分析】根据概率的求法，找准两点：①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率。因此，从袋中任意摸出一个球是白球的概率是3/10。

　　5.学校组织七、八、九年级同学参加某项综合实践活动.如图所示的扇形统计图表示上述各年级参加人数的分布情况.已知九年级有80人参加，则这三个年级参加该项综合实践活动共有 ▲ 人

　　【答案】320。

　　【考点】扇形统计图，频数、频率和总量的关系。

　　【分析】由已知和扇形统计图知九年级有80人参加，占25%，根据频数、频率和总量的关系得这三个年级参加该项综合实践活动的人数为80÷25%=320(人)。

　　6.在“情系玉树献爱心”捐款活动中，某校九(1)班同学人人拿出自己的零花钱，现将同学们的捐款数整理成统计表，则该班同学平均每人捐款 ▲ 元.

　　【答案】18。

　　【考点】平均数。

　　【分析】平均数是指在一组数据中所有数据之和再除以数据的个数。因此，

　　该班同学平均每人捐款数=18(元)。

　　7.某校艺术节演出中，5位评委给某个节目打分如下：9分，9.3分，8.9分，8.7分，9.1分，则该节目的平均得分是　 ▲ 　分.

　　【答案】9。

　　【考点】平均数。

　　【分析】平均数是指在一组数据中所有数据之和再除以数据的个数，因此该节目的平均得分是：( 9+9.3+8.9+8.7+9.1)÷ 5=9。

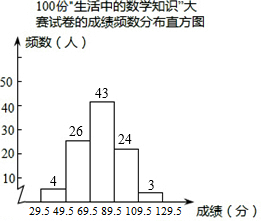
　　8.赵老师想了解本校“生活中的数学知识”大赛的成绩分布情况，随机抽取了100份试卷的成绩(满分为120分，成绩为整数)，绘制成下图所示的统计图。由图可知，成绩不低于90分的共有 ▲ 人.

　　【答案】27。

　　【考点】频数分布直方图。

　　【分析】如图所示，89.5～109.5段的学生人数有24人，109.5～129.5段的学生人数有3人，所以，成绩不低于90分的共有24+3=27人。