第五章 回归与相关
第一节 直线回归
一、直线回归的概念
当观察到两变量的成对数值,点在直角坐标上,点的趋向呈直线形状时,可对这两个变量间的联系用一个方程式进行表达。这种分析方法称为直线回归分析;这一方程式称为直线回归方程式。
二、直线回归方程式的一般表达式及其意义
1、方程的一般表达式

2、意义:
(1)a:回归直线在Y轴上的截距
a>0:直线与Y轴的交点在原点的上方;
a=0:直线通过原点;
a<0:直线与Y轴的交点在原点的下方;
(2)b:为回归系数, 即直线的斜率
b>0:Y随X增大而增大;
b<0:Y随X的增大而减少;
b=0:直线与X轴平行
b的统计学意义是:X每增(减)一个单位,Y平均改变b个单位
三、直线回归分析的步骤
1、收集成对的的实际数据,确定其中一个为自变量X,另一个为应变量Y;
2、将各对数据点在直角坐标上,得散点图,如散点呈直线趋势,则可作直线回归分析;
3、直线回归方程的求解,即求出a和b
(1)求解原理:最小二乘法-使各实测点至直线的纵向距离
的平方和最小。
(2)求解公式
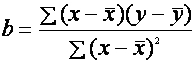 =
=
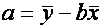
4、检验样本b是否从H0:β=0的总体中抽出
如以α=0.05为水准,则:
(1)当 P≤0.05时,不接受H0:β=0的假设,说明存在回归关系,方程成立,列出回归方程。
(2)当P>0.05时,接受H0:β=0的假设,方程不成立。
12
相关推荐
- 2016-11-18·2017公共卫生医师考试《生理学》复习笔记:第十章生殖
- 2016-11-18·2017公共卫生医师考试《生理学》复习笔记:第九章内分泌
- 2016-11-17·2017公卫执业医师_卫生毒理学章节考点汇总
- 2016-11-17·2017公共卫生执业医师《社会医学》复习:第一章绪论
- 2016-11-16·2017公共卫生医师考试《生理学》复习笔记:第八章神经系统的功能
热点推荐»
- 12016-09-212016公共卫生执业医师考试内容:接种异常反应
- 22016-09-212016公共卫生执业医师考试内容:毒理学定义|分类
- 32016-09-212016公共卫生执业医师考试内容:随机变量的定义
编辑推荐
examw.cn
-
2016年环球网校临床执业医师考试辅导单科基础强化班招生¥50.00
-
2016年环球网校临床执业医师考试辅导班次报名¥200.00
-
2016年环球网校临床执业医师考试辅导精品套餐报名¥650.00
-
2016年环球网校临床助理医师考试辅导单科基础强化班招生¥50.00
-
2016年环球网校临床助理医师考试辅导全科辅导班报名¥200.00
- 1
- 2
- 3
- 4
- 5
- 模拟试题
- 历年真题
- 考试题库





