某流感疫苗生产商的车间设备因寿命期已到需要更新，请用费用年值法比较选择设备更新的最优方案

简答题 某流感疫苗生产商的车间设备因寿命期已到需要更新，有A、B两种新设备可供选择。两种设备的经济数据见表2-3，设备投资发生在年初。财务基准收益率取15%。

某地区流感发病率逐日上升，为此当地政府制定了三种疫苗接种方案，计算期均设为5年。根据咨询人员分析论证，项目效果表现为减少发病人数，同时也减少了治疗费用，数据见表2-4；各方案每年投入的费用额见表2-5。设定折现率为3%。



【问题】
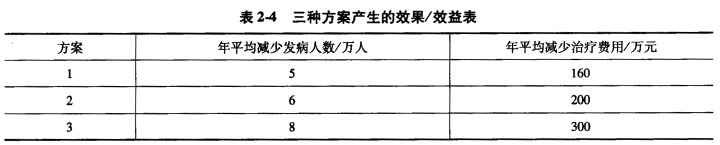
1.如果你是该企业的咨询人员，请用费用年值法比较选择设备更新的最优方案。
2.如果设备B的使用寿命期为9年，最后三年经营成本均为7000万元，期末净残值为2000万元，其他数据不变。请以最小寿命期作为共同研究期，比较选择最优方案。
3.咨询人员拟采用费用现值法来评价三种疫苗接种方案的优劣，请判断该方法是否妥当？说明理由。
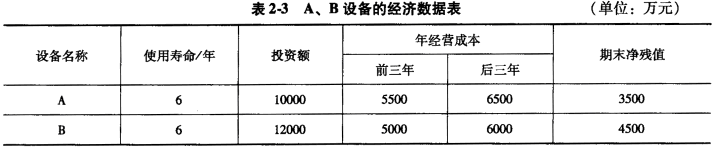
4.请对三种疫苗接种方案进行比选，哪种方法为最优方案（设定基准指标［C/E］o=400，即每减少发病一人需要花费400元）。

参考答案：

【解答】
1.AC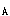=［10000+5500(P/A,15%,3)+6500(P/A,15%,3)(P/F,15%,3)-3500(P/F,15%,6)］×(A/P,15%,6)=(10000+12557.6+9757.826-1513.05)×0.26424=8139.22万元
AC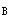=［12000+5000(P/A,15%,3)+6000(P/A,15%,3)(P/F,15%,3)-4500(P/F,15%,6)］×(A/P,15%,6)=(12000+11416+9007.224-1945.35)×0.26424=8053.47万元
经比较得知，费用年值较小的B方案较优。
2.PC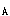=10000+5500(P/A,15%,3)+6500(P/A,15%,3)(P/F,15%,3)-3500(P/F，15%，6)=10000+12557.6+9757.826-1513.05=30802.38万元
PC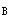=［12000+5000(P/A,15%,3)+6000(P/A,15%,3)(P/F,15%,3)+7000(P/A,15%,3)(P/F,15%,6)-2000(P/F,15%,9)］×(A/P,15%,9)(P/A,15%,6)=(12000+11416+9007.224+6909.192-568.6)×0.2096×3.7845=30748.67万元
经比较得知，费用现值较小的B方案较优。
3.采用费用现值法来评价三种方案的优劣是不妥当的，因为该法适用于效益相同或效益基本相同但难于具体估算的互斥方案的比较，但本题疫苗接种方案产生的货币化效益（减少治疗费用）不是该政府项目目标的主体，其主要效果表现为减少发病人数（难于货币量化），所以适合采用费用效果分析方法。
4.利用各备选方案效果和费用数据，因两者均不固定，所以应采用增量分析方法。
(1)各方案每年产生的效果年值见表24。
(2)各方案每年投入的费用年值：
方案1=［1300×(P/F,3%,1)+1400×(P/F,3%,2)+…+1800×(P/F,3%,5)］×(A/P，3%，5)=1532.36万元
方案2=［2200×(P/F,3%,1)+2300×(P/F,3%,2)+…+3200×(P/F,3%,5)］×(A/P，3%，5)=2644.14万元
方案3=［2500×(P/F,3%,1)+2600×(P/F,3%,2)+…+3600×(P/F,3%,5)］×(A/P，3%，5)=2962.98万元
(3)按方案费用年值由小到大排队，计算各方案的费用效果比：
方案1=1532.36/5=306.47元/人
方案2=2644.14/6=440.69元/人
方案3=2962.98/8=370.37元/人
方案2的费用效果比高于基准指标，应予放弃。
(4)计算方案1和3的增量费用效果比：△C/△E=（2962.98-1532.36)/(8-5)=476.87元
1人因两者增量费用效果比高于设定的基准值400，说明费用低的方案1为最优方案。

查看试题解析 进入焚题库

相关知识：二、涉及《工程项目组织与管理》的内容