ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图

简答题 ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图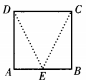，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

参考答案：二面角为30°，PE与面ECS成60角°

答案解析:（1）求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出（由二面角的平面角的定义）。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。
（2）求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线（直线PE）和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。
设CD的中点为F，练PF，EF
∵PC=PD，EC=ED
∴PF⊥CD，EF⊥CD（三垂线定理）
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC，PE⊥CD
∴PE⊥平面PCD，又PF在平面PCD内
∴PE⊥PF
设正方形边长为1（如图）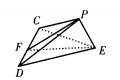

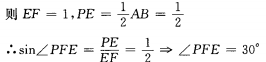
故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。

登录查看解析 进入题库练习

相关知识：第十五章、直线和平面