类型:学习教育
题目总量:200万+
软件评价:
下载版本
问答题【2014年真题】求(3x+1)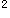 -4=0方程中的值解:(3x+1)
-4=0方程中的值解:(3x+1)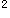 -4=0 移项(3x+1)
-4=0 移项(3x+1)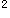 =4 开平方3x+1=2 移项3x=1 所以x=
=4 开平方3x+1=2 移项3x=1 所以x=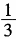 问题: (1)该同学的解题过程哪步错了?分析其原因。 (2)针对该生情况,请你设计一个辅导教学片段(可以为师生问答形式),并说明设计意图。 (3)除了开方法外,本题还可以用哪些方法解答(至少列举两种)?
问题: (1)该同学的解题过程哪步错了?分析其原因。 (2)针对该生情况,请你设计一个辅导教学片段(可以为师生问答形式),并说明设计意图。 (3)除了开方法外,本题还可以用哪些方法解答(至少列举两种)?
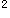 -4=0方程中的值解:(3x+1)
-4=0方程中的值解:(3x+1)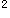 -4=0 移项(3x+1)
-4=0 移项(3x+1)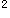 =4 开平方3x+1=2 移项3x=1 所以x=
=4 开平方3x+1=2 移项3x=1 所以x=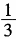 问题: (1)该同学的解题过程哪步错了?分析其原因。 (2)针对该生情况,请你设计一个辅导教学片段(可以为师生问答形式),并说明设计意图。 (3)除了开方法外,本题还可以用哪些方法解答(至少列举两种)?
问题: (1)该同学的解题过程哪步错了?分析其原因。 (2)针对该生情况,请你设计一个辅导教学片段(可以为师生问答形式),并说明设计意图。 (3)除了开方法外,本题还可以用哪些方法解答(至少列举两种)?参考答案:
(1)该同学在开平方3x+1=2这一步出现了错误,原因是对平方根的概念没有掌握。其次在最后得出根x=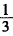 这一步也出现了错误,原因是对一元二次方程根的个数及写法没有掌握。 (2)师:3
这一步也出现了错误,原因是对一元二次方程根的个数及写法没有掌握。 (2)师:3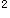 =?,(-3)
=?,(-3)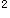 =? 生:9 师:根据平方根的定义,9的平方根为多少?生:±3 师:a(a≥0)的平方根为多少?生:当a>0时,平方根有两个
=? 生:9 师:根据平方根的定义,9的平方根为多少?生:±3 师:a(a≥0)的平方根为多少?生:当a>0时,平方根有两个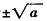 当a=0时,平方根为0 (由数字到字母,由具体到抽象,让学生理解平方根的概念及掌握开平方运算) 师:x
当a=0时,平方根为0 (由数字到字母,由具体到抽象,让学生理解平方根的概念及掌握开平方运算) 师:x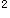 =16,x=? 生:±4 师:本题中(3x+1)
=16,x=? 生:±4 师:本题中(3x+1)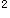 -4=0,开平方那一步怎么运算,可以得到几个答案,也就是有几个根?生:3x+1=2或3x+1=-2,可以得到两个答案,本题有两个不相等的实数根。师:(2x+3)
-4=0,开平方那一步怎么运算,可以得到几个答案,也就是有几个根?生:3x+1=2或3x+1=-2,可以得到两个答案,本题有两个不相等的实数根。师:(2x+3)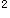 -16=0这个题目请写出完整的步骤。生:解:(2x+3)
-16=0这个题目请写出完整的步骤。生:解:(2x+3)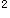 -16=0 移项(2x+3)
-16=0 移项(2x+3)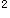 =16 开平方2x+3=4或2x+3=-4 移项2x=1或2x=-7 所以方程的两根为
=16 开平方2x+3=4或2x+3=-4 移项2x=1或2x=-7 所以方程的两根为 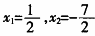 师:非常好。步骤也很完整。以后注意细节,继续努力。 (由易到难,由浅入深,让学生能运用开平方法解方程) 在整个辅导教学片段中,通过师生问答形式,根据学生已有的知识提出问题,启发学生反思自己做题中的错误以及错误的原因所在,帮助学生真正领悟开平方法解方程的正确解题方法,并通过巩固练习的方式,一步一步,由易到难,由具体到抽象促进能力的提高。 (3)①公式法:解:(3x+l)
师:非常好。步骤也很完整。以后注意细节,继续努力。 (由易到难,由浅入深,让学生能运用开平方法解方程) 在整个辅导教学片段中,通过师生问答形式,根据学生已有的知识提出问题,启发学生反思自己做题中的错误以及错误的原因所在,帮助学生真正领悟开平方法解方程的正确解题方法,并通过巩固练习的方式,一步一步,由易到难,由具体到抽象促进能力的提高。 (3)①公式法:解:(3x+l)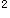 -4=0 3x
-4=0 3x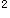 +2x-1=0 a=3,b=2,c=-1 △=b
+2x-1=0 a=3,b=2,c=-1 △=b -4ac=16>0 方程有两个不相等的实数根
-4ac=16>0 方程有两个不相等的实数根 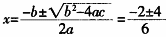 即:x
即:x =1,x
=1,x =
=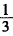 ②因式分解法:(3x+1)
②因式分解法:(3x+1)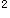 -4=0,因式分解得:(3x+3)(3x-1)=0,于是得:3x+3=0或3x-1=0 x
-4=0,因式分解得:(3x+3)(3x-1)=0,于是得:3x+3=0或3x-1=0 x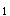 =-1,x
=-1,x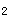 =
=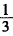
相关题库
| 题库产品名称 | 试题数量 | 优惠价 | 免费体验 | 购买 |
|---|---|---|---|---|
| 2021教师资格证《初中数学》考试题库 | 379题 | ¥29.00 | 免费体检 | 立即购买 |

微信扫码关注焚题库
-
历年真题
历年考试真题试卷,真实检验
-
章节练习
按章节做题,系统练习不遗漏
-
考前试卷
考前2套试卷,助力抢分
-
模拟试题
海量考试试卷及答案,分数评估

