单项选择题 潜水艇在水中下沉时,其所受阻力与下沉速度成正比,若潜艇由静止状态开始下沉,则在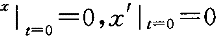 时,x(t)的方程是:
时,x(t)的方程是:
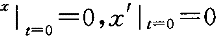 时,x(t)的方程是:
时,x(t)的方程是:A.x(t)=(mg/K)t
B.x(t)(-m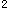 g/K
g/K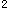 +(m
+(m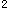 g/K
g/K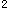 )
)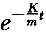
C.x(t)(-m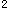 g/K
g/K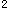 +(m
+(m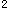 g/K
g/K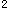 )
)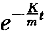 +(mg/K)t
+(mg/K)t
D.x(t)=(mg/K)t+(m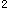 g/K
g/K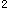 )
)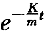
正确答案:C
答案解析:按微分方程的类型求出特解。解法如下由m(d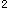 x/dt
x/dt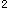 )=mg-K(dx/dt),可推出m(d
)=mg-K(dx/dt),可推出m(d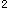 x/dt
x/dt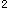 )+K(dx/dt)=mg,知微分方程为二阶常系数线性非齐次方程。求对应齐次方程的通解 M(d
)+K(dx/dt)=mg,知微分方程为二阶常系数线性非齐次方程。求对应齐次方程的通解 M(d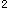 x/dt
x/dt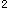 )+K(dx/dt)=0,mr
)+K(dx/dt)=0,mr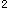 +Kr=0,r
+Kr=0,r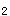 =-K/m x=c
=-K/m x=c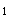 +c
+c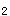
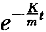 设非齐次方程的特解
设非齐次方程的特解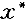 =at,则
=at,则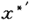 =a,
=a,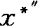 =0,代入非齐次方程得 0+Ka=mg
=0,代入非齐次方程得 0+Ka=mg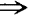 a=Ka/mg 将a=mg/K代入,得
a=Ka/mg 将a=mg/K代入,得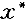 =(mg/K)t 通解为x=c
=(mg/K)t 通解为x=c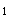 +c
+c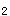
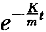 +(mg/K)t 代入初始条件t=0,x=0,得 0=c
+(mg/K)t 代入初始条件t=0,x=0,得 0=c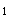 +c
+c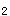 ,c
,c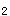 =-c
=-c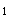 x′=-(K/m)c
x′=-(K/m)c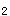
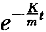 +mg/K 代入初始条件t=0,x′
+mg/K 代入初始条件t=0,x′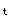 =0,得 0=-(K/m)c
=0,得 0=-(K/m)c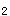 +mg/K,(K/m)c
+mg/K,(K/m)c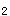 =mg/K,c
=mg/K,c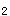 =m
=m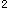 g/K
g/K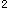 ,c
,c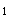 =-m
=-m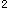 g/K
g/K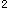 通解为x=-m
通解为x=-m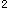 g/K
g/K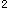 +(m
+(m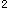 g/K
g/K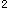 )
)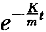 +(mg/K)t
+(mg/K)t
相关知识:一、高等数学
考试题库
- ·2020年一级结构工程师《专业考试》考试题库我要购买
- ·2020年二级结构工程师《专业考试》考试题库我要购买
- ·2020年一级结构工程师《基础考试》考试题库我要购买
- ·2020年一级结构工程师《全科》考试题库我要购买
热点推荐»
- 12020-06-29厦门2020年结构工程师报名时间预计8月份
- 22020-06-292020年武汉二级结构工程师报考条件
- 32020-06-292020广州结构工程师报名入口:中国人事考试网
编辑推荐
- 考试题库
- 模拟试题
- 历年真题
