类型:学习教育
题目总量:200万+
软件评价:
下载版本
简答题 求由曲线y=2-x2,y=2x-1及x≥0围成的平面图形的面积S以及此平面图形绕x轴旋转一周所得旋转体的体积Vx。
参考答案:本题考查的知识点有平面图形面积的计算及旋转体体积的计算。
本题的难点是根据所给的已知曲线画出封闭的平面图形,然后再求其面积S。求面积的关键是确定对x积分还是对y积分。
确定平面图形的最简单方法是:题中给的曲线是三条,则该平面图形的边界也必须是三条,多一条或少一条都不是题中所要求的。
确定对x积分还是对y积分的一般原则是:尽可能用一个定积分而不是几个定积分之和来表示。本题如改为对y积分,则有 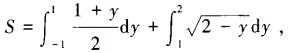
计算量显然比对x积分的计算量要大,所以选择积分变量的次序是能否快而准地求出积分的关键。
在求旋转体的体积时,一定要注意题目中的旋转轴是x轴还是y轴。
由于本题在x轴下面的图形绕x轴旋转成的体积与x轴上面的图形绕x轴旋转的旋转体的体积重合了,所以只要计算x轴上面的图形绕x轴旋转的旋转体体积即可。如果将旋转体的体积写成 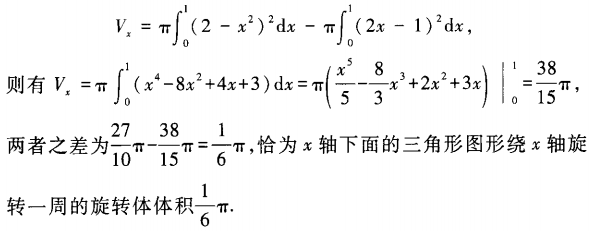
上面的这种错误是考生比较容易出现的,所以审题时一定要注意。
解 由已知曲线画出平面图形为如图2-1-2所示的阴影区域。 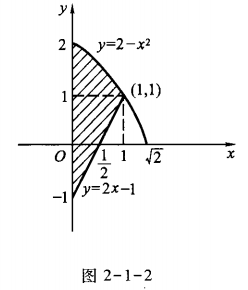

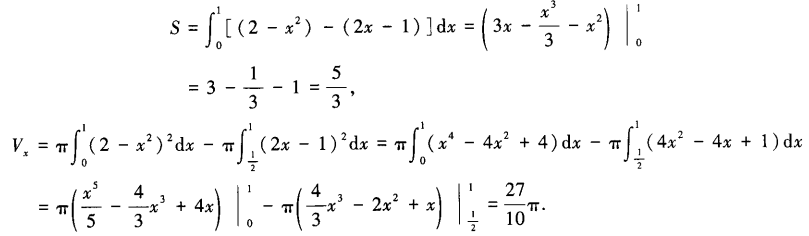
答案解析:
相关题库
| 题库产品名称 | 试题数量 | 优惠价 | 免费体验 | 购买 |
|---|---|---|---|---|
| 2022年成人高考《英语+政治+高等数学二(专 | 3215题 | ¥235 | 免费体验 | 立即购买 |
| 2022年成人高考《高等数学二(专升本)》考 | 880题 | ¥98 | 免费体验 | 立即购买 |

微信扫码关注焚题库
-
历年真题
历年考试真题试卷,真实检验
-
章节练习
按章节做题,系统练习不遗漏
-
考前试卷
考前2套试卷,助力抢分
-
模拟试题
海量考试试卷及答案,分数评估

