类型:学习教育
题目总量:200万+
软件评价:
下载版本
相关题库
| 题库产品名称 | 试题数量 | 优惠价 | 免费体验 | 购买 |
|---|---|---|---|---|
| 2022年成人高考《文科数学(高起点)》考试 | 518题 | ¥98 | 免费体验 | 立即购买 |
| 2022年成人高考《英语+文科数学+语文+史地综 | 3102题 | ¥314 | 免费体验 | 立即购买 |
| 2022年成人高考《英语+文科数学+语文》考试 | 2066题 | ¥235 | 免费体验 | 立即购买 |

微信扫码关注焚题库
-
历年真题
历年考试真题试卷,真实检验
-
章节练习
按章节做题,系统练习不遗漏
-
考前试卷
考前2套试卷,助力抢分
-
模拟试题
海量考试试卷及答案,分数评估


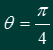 时,判断该圆与直线y=x的位置关系.
时,判断该圆与直线y=x的位置关系.
