类型:学习教育
题目总量:200万+
软件评价:
下载版本
问答题
设F(x)=f(x)g(x),其中函数f(x),g(x)在(-∞,+∞)内满足以下条件: f′(x)=g(x),g′(x)=f(x),且f(0)=0,f(x)+g(x)=2e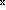 。
。
(1)求F(x)所满足的一阶微分方程;
(2)求出F(x)的表达式。
参考答案:
题目要求F(x)所满足的微分方程,而微分方程中含有其导函数,自然想到对F(x)求导,并将其余部分转化为用F(x)表示,导出相应的微分方程,然后再求解相应的微分方程即可。
(1)由F(x)=f(x)g(x),有 F′(x)=f′(x)g(x)+f(x)g′(x)=g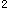 (x)+f
(x)+f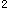 (x) [f(x)g(x)]
(x) [f(x)g(x)]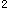 -2f(x)g(x)=(2e
-2f(x)g(x)=(2e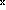 )
)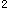 -2F(x) 可见F(x)所满足的一阶微分方程为 F′(x)+2F(x)=4e
-2F(x) 可见F(x)所满足的一阶微分方程为 F′(x)+2F(x)=4e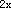 相应的初始条件为F(0)=f(0)g(0)=0
相应的初始条件为F(0)=f(0)g(0)=0
(2)由题(1)得到F(x)所满足的一阶微分方程,求F(x)的表达式只需解一阶微分方程,又一阶线性非齐次微分方程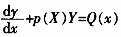 的通解为
的通解为 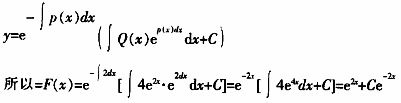 将F(0)代入上式,得C=-1 所以F(x)=e
将F(0)代入上式,得C=-1 所以F(x)=e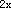 -e
-e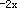
相关题库
| 题库产品名称 | 试题数量 | 优惠价 | 免费体验 | 购买 |
|---|---|---|---|---|
| 2021教师资格证《初中数学》考试题库 | 379题 | ¥29.00 | 免费体检 | 立即购买 |

微信扫码关注焚题库
-
历年真题
历年考试真题试卷,真实检验
-
章节练习
按章节做题,系统练习不遗漏
-
考前试卷
考前2套试卷,助力抢分
-
模拟试题
海量考试试卷及答案,分数评估

