2021年二级注册建筑师《建筑结构与建筑设备》教材精讲：第三章

　　第三章、建筑力学

　　一、平面汇交力系的合成与平衡

　　平面汇交力系是指各力的作用线均在同一平面且交于同一点的力系。平面汇交力系可简化为一个合力，合力的大小与方向等于各分力的矢量和，合力的作用线通过汇交点。包含 n 个力的汇交力系的合力矢为：

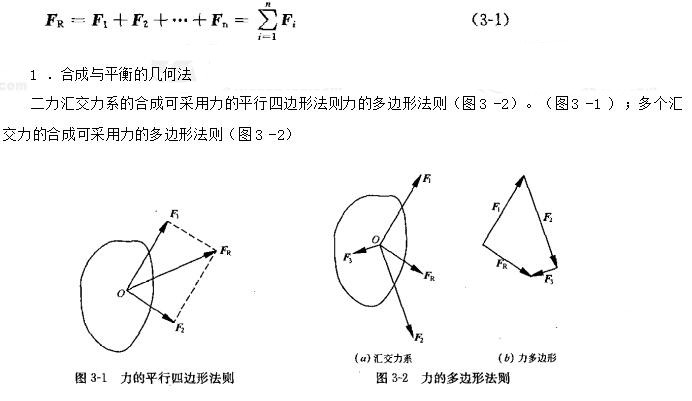
　　　平面汇交力系平衡的充分和必要条件是：

　　该力系的合力矢等于零。若采用几何法，则平衡的充分和必要条件(即几何条件)是：该力系的力多边形自行封闭。

　　2.合成与平衡的解析法

　　力在坐标轴上的投影：力在某坐标轴上的投影等于力的大小乘以力与坐标轴正向间夹角的余弦。

　　合力投影定理：合力矢在某一轴上的投影等于各分力矢在同一轴上投影的代数和。

　　如图 3-3 所示，：以汇交力系的汇交点 O 作为坐标原点，建立直角坐标系工伪。设各分力矢在 x 、 y 坐标轴上的投影分别为 X1 、 X2 ： … Xn和 Y1 、Y2…Yn(图3-3a ) ，则合力矢在 x 、 y 轴上的投影(图3-3b)为：

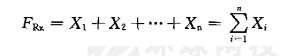
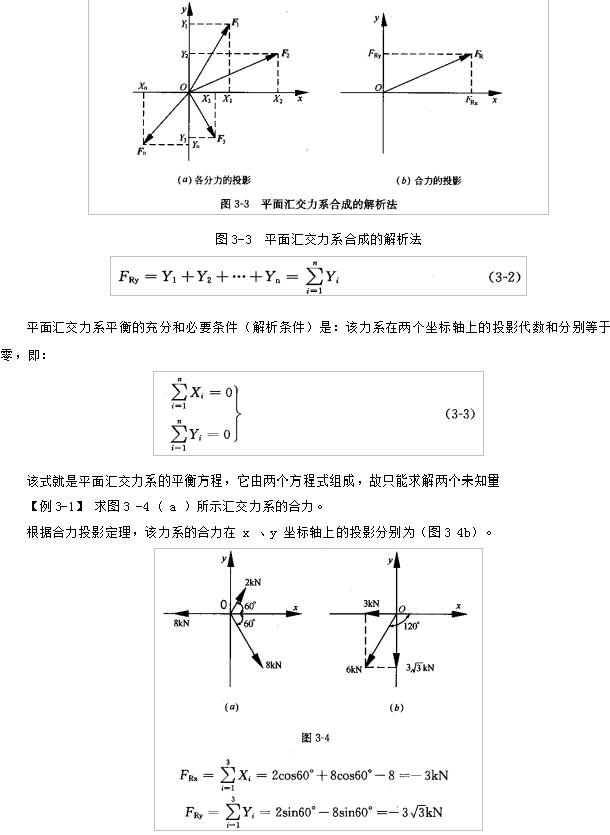
　　故合力 FR 的大小为：

　　二、平面任意力系的简化与平衡

　　平面任意力系是指各力的作用线均在同一平面但呈任意分布的力系。

　　力的平移定理：可以将作用在刚体上点 A 的力 F 平移到任一点 B ，但必须同时附加一个力偶，该力偶的力矩等于原来的力 F 对新作用点 B 的矩。

　　合力矩定理：平面任意力系的合力对作用面内任一点的矩，等于力系中各力对同一点的矩的代数和。

　　平面任意力系向作用面内任一点 O 简化，可得到一个力和一个力偶(图 3 -6 )。这个力等于该力系的主矢(即各力的矢量和)，作用线通过简化中心O;这个力偶的矩等于该力系对于点 O 的主矩(即各力对点 O 的矩的代数和)。

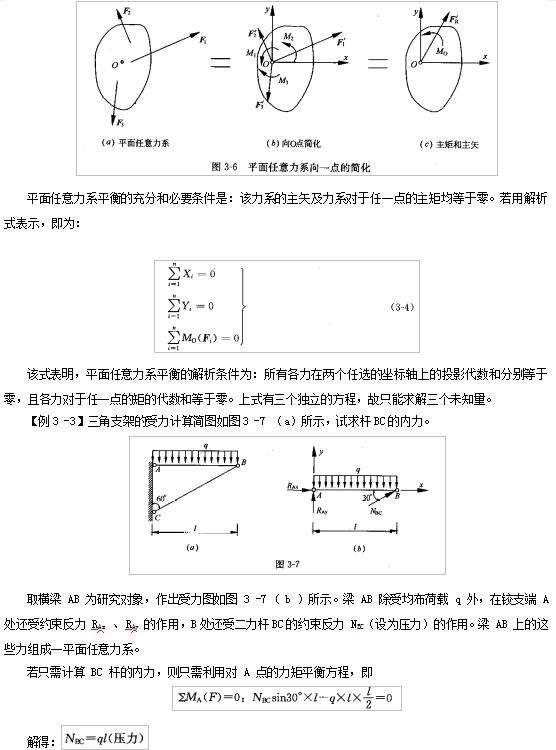
　　若还需进一步计算 A 点的约束反力，则可利用对 x 、y 轴的投影平衡方程，即

　　解方程得：