1.某商场门口停了自行车、三轮车和小轿车共44辆,车轮一共l41个。已知小轿车比三轮车的2倍少l辆,那么这个商场门口三轮车有多少辆?
A.11.
B.12.
C.21.
D.22.
【答案】A
【解析】设自行车、三轮车和小轿车各有x,y,2y-1辆,则
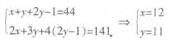
2.把同一排6张座位编号为l,2,3,4,5,6的电影票全部分给4个人,每人至少分l张,至多分2张.且这两张票具有连续的编号,那么不同的分法种数是:
A.168.
B.96.
C.72.
D.144.
【答案】D
【解析】【答案】D。

3.C是线段AB上一点,D是线段CB的中点,已知图中所有线段的长度之和为23。线段AC和线段CB的长度都是正整数,那么线段AC的长度为:

A.2.
B.3.
C.5.
D.7.
【答案】B

4.某班进行一次考试,其中得优的同学平均分数为95分,未得优的同学平均分数为80分,现在已知全班的平均分数不低于92分,请问得优的同学占全班的比重至少为多少?
A.66.7%
B.75%
C.80%
D.90%
【答案】C
【解析】设全班人数为1,得优的同学人数为x,未得优的同学人数为1-x,则95x+80(1-x)≥92,则x≥80%。
5.某茶叶店运到一批一级茶、二级茶和三级茶,其中二级茶的数量是一级茶的2倍,三级

A.40.
B.45.
C.50.
D.55.
【答案】B
【解析】【答案】B。

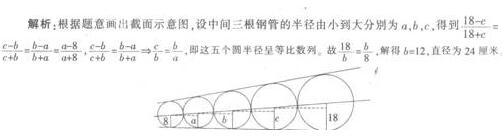
6.甲、乙两人玩纸牌游戏,从足够数量的纸牌中取牌。规定每人最多两种取法,甲每次取4张或(4-k)张,乙每次取6张或(6-k)张(k是常数,0 A.102张 B.108张 C.112张 D.116张 【答案】B 【解析】由于k在1~3之间取,所以4-k的范围在1~3之间,甲的牌数范围在1×15~4x15之间。同理,乙的牌数在3×16+6~6×17之间。根据二者牌数相等,比较这两个区间。 田 15-60 乙 54-102 重合区间 54-60 因此两人的牌数最少为54,总牌数至少有108张。 验证:乙每次取3张取16次,另外1次取6张牌,共取3x16+6=54张。甲每次取4张牌取13次,另外2次取1张牌,共取4x13+1×2=54张牌。故上述牌数最少情况真实存在。 7.A、B、C、D、E、F六个小朋友做游戏,每轮游戏都按照下面的箭头方向把原来手里的玩具传给另外一个小朋友:A→F,B→D,C→E,D→B,E→A,F→C。开始时,A、B、C、D、E、F拿着各自的玩具,传递完l0轮时,有几个小朋友又拿到了自己的玩具? A.2. B.3. C.4. D.5. 【答案】A 【解析】观察传递过程可以发现,B、D两个小朋友每经过2轮,玩具又回到自己手里,A、C、E、F四个小朋友需经过4轮,玩具才能回到各自手里。即B、D的玩具回到自己手里的周期是2轮,A、C、E、F的玩具回到自己手里的周期是4轮。 10÷2=5,是整周期,则B、D两位小朋友经过10轮后,玩具回到自己手里; 10÷4=2……2,不是整周期。则A、C、E、F四位小朋友经过10轮后,玩具不在自己手里。 故传递完10轮时.只有2个小朋友又拿到了自己的玩具。 8.某小学五年级的学生身高(按整数厘米计算),最矮的是138厘米,最高的是160厘米。如果任意从这些学生中选出若干人,那么,至少要选出多少人才能保证有5人的身高相同? A.89. B.92. C.93. D.97. 【答案】C 【解析】考虑最坏的情况,从最矮的138cm到最高的160cm每个整数厘米都有人,共160-138+1=23种身高值,且每种身高都先选出4人,共计23×4=92人,最后再任选一名学生能保证有5人的身高相同,所以至少要选出92+1=93人。 9.某工厂2月份产值比1月份的增加10%,3月份比2月份的减少10%,那么: A.3月份与1月份产值相等 【答案】B 【解析】设1月份产值为1,则2月份为1.1,3月份为1.1x0.9=0.99。1月份比3月份多1÷ 10.五根半径不同的钢管从细到粗彼此相切地摆在地面上,上面放一块木板与每根钢管都相切,若最细钢管半径为8厘米,最粗钢管半径为l8厘米,则最中间的钢管直径为: A.10厘米 B.12厘米 C.20厘米 D.24厘米 【答案】D 【解析】【答案】D。

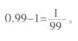
- 2018-05-132018年招警考试《行测》每日一练习题5.13
- 2018-05-082018年招警考试公安基础每日一练习题5.8
- 2018-05-022018年招警考试公安基础每日一练习题5.2
- 2018-05-022018年招警考试《行测》每日一练习题5.2
- 2018-05-012018年招警考试《行测》每日一练习题5.1
-
12018-03-312018年招警考试行测每日一练习题3月汇总
-
22018-03-012018年招警考试行测每日一练习题2月汇总
-
32018-03-012018年招警考试行测每日一练习题1月汇总
编辑推荐
- 模拟试题
- 历年真题
