2020咨询工程师考试《方法实务》模拟题库（6）_第2页

　　参考答案：(1)建立回归模型。经过分析，发现该地区镀锌钢板消费量与第二产业产值之间存在线性关系，将镀锌钢板设为因变量y，以第二产业产值为自变量x，建立一元回归模型：

　　y=a+bx

　　(2)计算参数。采用最小二乘法，计算出相关参数：

　　3)相关检验。

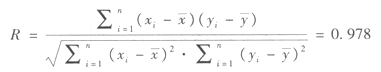
　　在α=0.05时，自由度=n-2=10-2=8，查相关系数表，得R0.05=0.632。

　　因为R=0.978>0.632=R0.05，故在α=0.05的显著性检验水平上，检验通过，说明第二产业产值与镀锌钢板需求量线性关系合理。相关计算见下表。

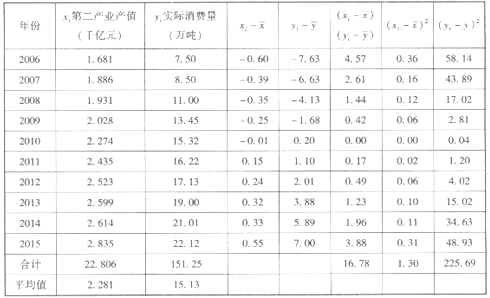
　　注：本表尾数误差系计算机自动圆整所致，因而手算结果与机算会有误差。

　　(4)t检验。

　　在α=0.05时，自由度=n-2=10-2=8，查t检验表，得t(α/2，8)=t(0.025，8)=2.306。

　　因为tb=13.309>2.306=t(0.025，8)，故在α=0.05的显著性检验水平上，t检验通过，说明第二产业产值与镀锌钢板需求量线性关系明显。

　　年当地第二产业年增长速度为7%，则2020年地区第二产业产值将达到：

　　x(2020)=(1+r)5×x2015=(1+7%)5X2.835=3.976(千亿元)

　　于是，2020年当地镀锌钢板需求点预测为：

　　y(2020)=a+bx(2020)=-14.23+12.869×3.976=36.94(万吨)

　　区间预测：

　　于是，在α=0.05的显著性检验水平上，2020年镀锌钢板需求量的置信区间为：

　　即有95%的可能性在(32.31，41.57)的区间内。