
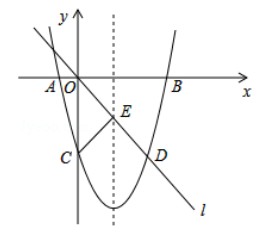
如图,在平面直角坐标系中,已知抛物线y=ax²+bx-8与x轴交于A, B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0), (6,-8)
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE2相似于FCE?若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0, m),直线PB与直线1交于点Q,试探究:当m为何值时,△OPQ是等腰三角形。
(1)∵抛物线y=ax2+bx-8经过点A(-2,0),D(6,-8),
∴4a-2b-8=0;36a+6b-8=-8
解得 a=1/2;b=-3
∴抛物线的函数表达式为y=1/2x²-3x-8;
∵y= 1/2x²-3x-8=1/2(x-3)²- 25/2
∴抛物线的对称轴为直线x=3.
又抛物线与x轴交于A,B两点,点A的坐标为(-2,0).
∴点B的坐标为(8,0),
设直线l的函数表达式为y=kx.
∵点D(6,-8)在直线l上,
∴6k=-8,解得k=-4/3,
∴直线L的函数表达式为y=-4/3x,
∵点E为直线L和抛物线对称轴的交点,
∴点E的横坐标为3,纵坐标为-4/3×3=-4,
∴点E的坐标为(3,-4);
(2)抛物线上存在点F,使△FOE≌△FCE.
∵OE=CE=5,
∴FO=FC,
∴点F在OC的垂直平分线上,此时点F的纵坐标为-4,
∴ 1/2x²-3x-8=-4,解得x=3±√17
∴点F的坐标为(3- √17,-4)或(3+ √17,-4)
 ,我们将会及时处理。
,我们将会及时处理。