2021年中考数学压轴题精选（8）

　　1、已知:如图,抛物线y=-x²+bx+c与x轴、y轴分别相交于点A (-1, 0)、B(0，3)两点，顶点为D.

　　(1) 求该抛物线的解析式;

　　(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;

　　(3) △AOB与△BDE是否相似?如果相似，请予以证明;如果不相似，请说明理由.

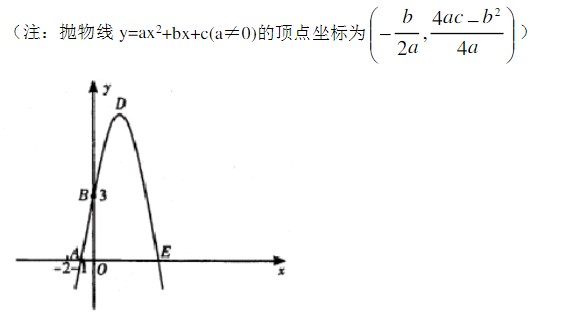
　　解: (1)由己知得:c=3,-1-b+C=0

　　解得c=3,b=2

　　∴抛物线的线的解析式为y=-x²+2x+3

　　(2)由顶点坐标公式得顶点坐标为(1, 4)

　　所以对称轴为x=1,A,E关于x=1对称，所以E(3, 0)

　　设对称轴与x轴的交点为F

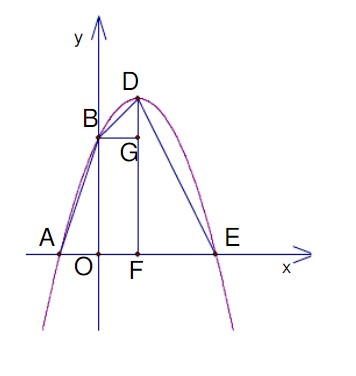
　　(3)相似

　　如图，BD=√BG² +DG² =√1²+1²=2

　　BE=√BO²+OE²=√3²+3²=3√2

　　DE=√DF²+EF² =√2² +4² =2√5

　　所以BD²+ BE²=20，DE²=20 即: BD² + BE²= DE²,所以△BDE是直角三角形

　　所以∠AOB=∠DBE=90°,且AO/BO=BD/BE=√2/2

　　所以△AOB: △DBE.