2021年中考数学压轴题精选（6）

　　如图，点C是以AB为直径的⊙O上的一点，AD与过点C的切线互相垂直，垂足为点D. 

　　(1)求证：AC平分∠BAD; 

　　(2)若CD=1，AC=根号10，求⊙O的半径长.

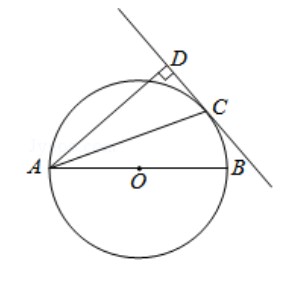
　　(1)证明：连接OC，

　　∵OA=OC，

　　∴∠ACO=∠CAO，

　　∵CD切⊙O于C，

　　∴CO⊥CD.

　　又∵AD⊥CD，

　　∴AD∥CO，

　　∴∠DAC=∠ACO，

　　∴∠DAC=∠CAO，

　　∴AC平分∠BAD;

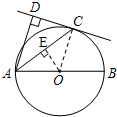
　　(2)解：过点O作OE⊥AC于E，

　　∵CD=3，AC=3 ，在Rt△ADC中，AD= =6，

　　∵OE⊥AC，∴AE= AC= ，

　　∵∠CAO=∠DAC，∠AEO=∠ADC=90°，

　　∴△AEO∽△ADC，

　　∴ ，即 ，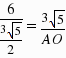

　　∴AO= ，即⊙O的半径为 .