1.已知二次函数y=x²-2mx+4m—8
(1)当x≤2时，函数值y随x的增大而减小，求m的取值范围。
(2)以抛物线y=x²-2mx+4m-8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M，N两点在抛物线上)，请问：△AMN的面积是与m无关的定值吗?若是，请求出这个定值;若不是，请说明理由。
(3)若抛物线y=x²-2mx+4m-8与x轴交点的横坐标均为整数，求整数m的值。
答案：
2、答案：解：(1)∵y=(x-m)²+4m-8-m²
∴由题意得，m≥2 (3分)
(2)根据抛物线和正三角形的对称性，可知MN⊥y轴，设抛物线的对称轴与MN交于点B，则AB⊥√3B。
设M(a，b)
∴ BM=a-m(m
又AB=yB-yA=b-(4m-8-m²)=a²-2am+4m-8-(4m-8-m²)=a²-2am+m²
∴a-m=√3
∴ BM=√3 ，AB=3
∴为定值 (3分)
(3)令y=0，即x²-2xm+4m-8=0时，有
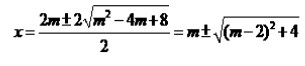
由题意，(m-2)²+4为完全平方数，令(m-2)²+4=n²
即(n+m-2)(m-m+2) =4
∵m,n为整数，n+m-2;m-m+2奇偶性相同，
∴综合得m=2
，我们将会及时处理。
