2019年桂林中考数学压轴题

2019年桂林中考数学压轴题

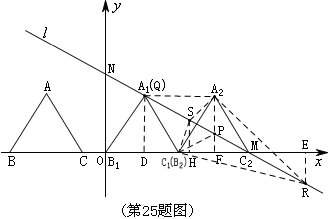
　　25.(12分)(桂林)如图，在平面直角坐标系中，有一条直线：与轴、轴分别交于点、，一个高为3的等边三角形，边在轴上，将此三角形沿着轴的正方向平移.

　　(1)在平移过程中，得到，此时顶点恰落在直线上，写出点的坐标 ;(4分)

　　(2)继续向右平移，得到，此时它的外心恰好落在直线上，求点的坐标;(4分)

　　(3)在直线上是否存在这样的点，与(2)中的、、任意两点能同时构成三个等腰三角形，如果存在，

　　求出点的坐标;如果不存在，说明理由. (4分)

　　参考答案

　　25.(本题满分12分)

　　(1) ………………………………4分

　　(2)设,连接并延长交轴于点,连接 ………………………5分

　　在等边三角形中,高

　　∴， ………………………………6分

　　∵点是等边三角形的外心

　　∴，∴ 即 ………………………………7分

　　将代人，解得：

　　∴ ………………………

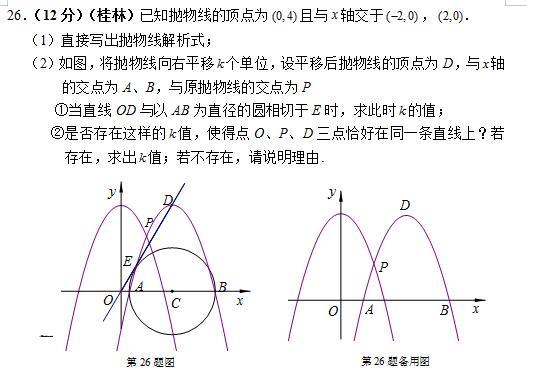
　　26.(12分)(桂林)已知抛物线的顶点为且与轴交于，.

　　(1)直接写出抛物线解析式;

　　(2)如图，将抛物线向右平移个单位，设平移后抛物线的顶点为D，与轴的交点为A、B，与原抛物线的交点为P

　　①当直线OD与以AB为直径的圆相切于E时，求此时的值;

　　②是否存在这样的值，使得点O、P、D三点恰好在同一条直线上?若存在，求出值;若不存在，请说明理由.

　　参考答案：

　　26.(本题满分12分)

　　解：(1) ............... 2分

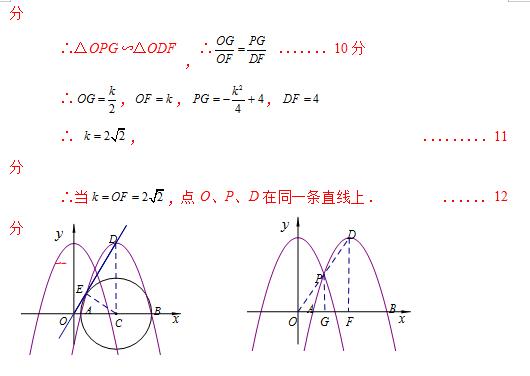
　　(2)连接CE, CD，

　　∵OD是⊙C的切线，∴CE⊥OD .......3分

　　在Rt△CDE中，∠CED=，CE=AC=2，DC=4，∴∠EDC=..4分

　　∴在Rt△CDO中，∠OCD=，CD=4，∠ODC=

　　∴ ..................6分

　　∴当直线OD与以AB为直径的圆相切时，. ...7分

　　(3) 设平移个单位后的抛物线的解析式是

　　它与交于点P，

　　可得点P的坐标是 ........8分

　　热点关注：2019年全国初三中考数学试题及答案汇总