2019年中级会计师财务管理考前密训习题二_第4页

　　四、计算分析题

　　1.某投资者计划2019年初购置一处现行市场价格为1000万元的房产。由于资金不足，房主提出了四种延期付款方案供其选择。

　　方案一：2020年至2029年，每年年初付款155万元。

　　方案二：2024年至2030年，每年年初付款310万元。

　　方案三：2019年至2029年，每年年初付款135万元。

　　方案四：2020年至2028年，每年年初付款150万元，2029年初再支付200万元。

　　已知银行贷款利率为8%，每年复利一次。

　　要求：

　　1)计算上述四个方案的付款额在2019年初的现值;

　　2)判断该投资者应选择哪个方案，并说明理由;

　　3)以该房产的现行市价为基础，计算方案一的内含利率。

　　【答案】

　　1)方案一付款额现值=155×(P/A，8%，10)=1040.07(万元)

　　方案二付款额现值=280×(P/A，8%，7)×(P/F，8%，4)=1071.48(万元)

　　方案三付款额现值=135×(P/A，8%，11)×(1+8%)=1040.87(万元)

　　方案四付款额现值=150×(P/A，8%，9)+200×(P/F，8%，10)=1029.68(万元)

　　2)由于方案四的付款额现值最低，因此应选择方案四。

　　3)采用插值法推算方案一的内含利率i1如下：

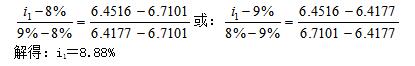
　　依据资料，有：155×(P/A，i1，10)=1000，整理，得：(P/A，i1，10)=1000/155=6.4516

　　由：(P/A，8%，10)=6.7101，(P/A,9%，10)=6.4177，根据“利率差之比=对应的系数差之比”的比例关系，列方程求解利率i1：

　　2.资产组合M的期望收益率为18%，标准离差为27.9%;资产组合N的期望收益率为13%，标准离差率为1.2。投资者张某和赵某决定将其个人资金投资于资产组合M和N中，张某期望的最低收益率为16%，赵某投资于资产组合M和N的资金比例分别为30%和70%。

　　要求：

　　1)计算资产组合M的标准离差率。

　　2)判断资产组合M和N哪个风险更大。

　　3)为实现其期望的收益率，张某应在资产组合M上投资的最低比例是多少?

　　【答案】

　　1)资产组合M的标准离差率=27.9%÷18%=1.55

　　2)资产组合M的标准离差率1.55大于资产组合N的标准离差率1.2，说明资产组合M的风险更大。

　　3)假设投资资产组合M的比例为X，依据资料，有：X×18%+(1-X)×13%=16%

　　解得：X=60%，即张某应在资产组合M上投资的最低比例是60%。