2018注册造价工程师《案例分析》预习题及答案（11）

2018注册造价工程师《案例分析》预习题及答案（11）

　　背景：

　　根据工作之间的逻辑关系，某工程施工网络计划如图2-7所示。该工程有两个施工组织方案，相应的各工作所需的持续时间和费用见表2-25。在施工合同中约定：合同工期为27 1天，实际工期每拖延1天，逾期违约金为0.5万元;实际工期每提前1天，提前工期奖为0.5万元。

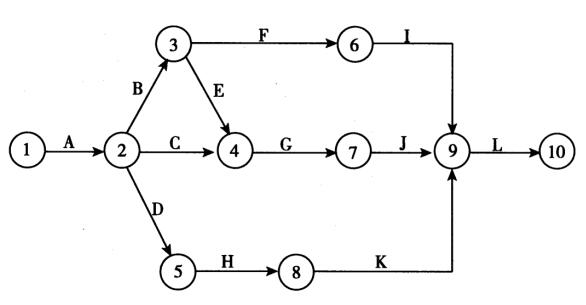
　　图2-7 某工程施工网络计划

　　表2-25 基础资料表

　　问题：

　　1.分别计算两种施工组织方案的工期和综合费用并确定其关键线路。

　　2.如果对该工程采用混合方案组织施工，应如何组织施工较经济?相应的工期和综合费用各为多少?(在本题的解题过程中不考虑工作持续时间变化对网络计划关键线路的影响)

　　分析要点：

　　本案例考核施工组织方案的比选原则和方法以及在费用最低的前提下对施工进度计划(网络计划)的优化。

　　问题1涉及关键线路的确定和综合费用的计算。若题目不要求计算网络计划的时间参数，而仅仅要求确定关键线路，则并不一定要通过计算网络计划的时间参数，按总时差为零的工作所组成的线路来确定关键线路;而可先列出网络计划中的所有线路，再分别计算各线路的长度，其中最长的线路即为关键线路。

　　所谓综合费用，是指施工组织方案本身所需的费用与根据该方案计算工期和合同工期的差额所产生的工期奖罚费用之和，其数值大小是选择施工组织方案的重要依据。

　　问题2实际上是对施工进度计划的优化。采用混合方案组织施工有以下两种可能性：一是关键工作采用方案Ⅱ(工期较短)，非关键工作采用方案I(费用较低)组织施工;二是在方案I的基础上，按一定的优先顺序压缩关键线路。通过比较以上两种混合组织施工方案的综合费用，取其中费用较低者付诸实施。

　　由于本工程非关键线路的时差天数很多，非关键工作持续时间少量延长或关键工作持续时间少量压缩不改变网络计划的关键线路，因此，本题出于简化计算的考虑，在解题过程中不考虑工作持续时间变化对网络计划关键线路的影响。但是，在实际组织施工时，要注意原非关键工作延长后可能成为关键工作，甚至可能使计划工期(未必是合同工期)延长;而关键工作压缩后可能使原非关键工作成为关键工作，从而改变关键线路或形成多条关键线路。需要说明的是，按惯例，施工进度计划应提交给监理工程师审查，不满足合同工期要求的施工进度计划是不会被批准的。因此，从理论上讲，当原施工进度计划不满足合同工期要求时，即使压缩费用大于工期奖，也必须压缩(当然，实际操作时，承包商仍可能宁可承受逾期违约金而按费用最低的原则组织施工)。另外还要注意，两种方案的关键线路可能不同，在解题时要注意加以区分。

　　答案：

　　问题1：

　　解：根据对图2-7施工网络计划的分析可知，该网络计划共有四条线路，即：

　　线路1：1-2-3-6-9-10

　　线路2：1-2-3 -4-7 -9-10

　　线路3：1-2-4-7-9-10

　　线路4：1-2-5-8-9-10

　　1.按方案I组织施工，将表2-25中各工作的持续时间标在网络图上，如图2-8所示。

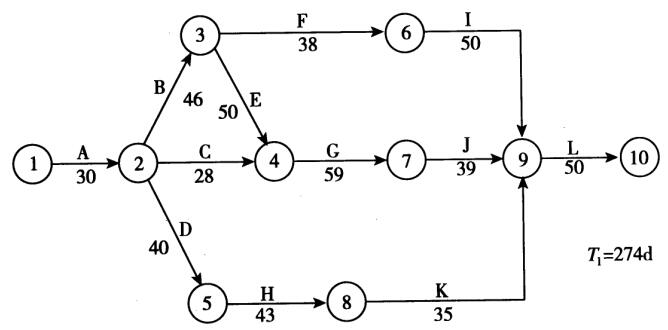
　　图2—8 方案I施工网络计划

　　图2-8中四条线路的长度分别为：

　　t1= 30+46+38+50+50=214 (d)

　　t2=30+46+50+59+39+50=274 (d)

　　t3=30+28+59+39+50=206 (d)

　　t4=30+40+43+35+50=198 (d)

　　所以，关键线路为1-2-3-4-7-9-10，计算工期T=274d。

　　将表2 -25中各工作的费用相加，得到方案I的总费用为212.5万元，则其综合费用C1=212.5+(274 - 271)×0.5=214(万元)。

　　2.按方案Ⅱ组织施工，将表2-25中各工作的持续时间标在网络图上，如图2-9所示。

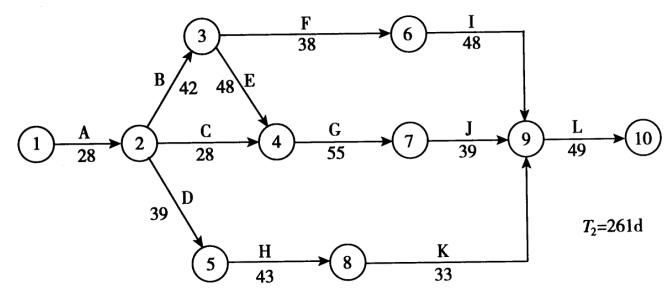
　　图2—9方案Ⅱ施工网络计划

　　图2-9中四条线路的长度分别为：

　　tl =28 +42 +38 +48 +49 =205 (d)

　　t2=28+42+48+55+39+49=261 (d)

　　t3 -28+28+55+39 +49=199 (d)

　　t4=28+39 +43+33 +49=192 (d)

　　所以，关键线路仍为1-2-3-4-7-9-10，计算工期咒=261d。

　　将表2-25中各工作的费用相加，得到方案Ⅱ的总费用为224.5万元，则其综合费用C2=224.5+(261 - 271)×0.5=219.5(万元)。

　　问题2：

　　解：1.关键工作采用方案Ⅱ，非关键工作采用方案I

　　即关键工作A、B、E、G、J、L执行方案Ⅱ的工作时间，保证工期为261d;非关键工作执行方案I的工作时间，而其中费用较低的非关键工作有：孟D =40d,cD=19万元;t1=50d,ci=24万元;参K=35d,CK=15万元。则，按此方案混合组织施工的综合费用为：

　　C,= 219.5 -(19.5- 19) - (25 -24)-(16 - 15)=217(万元)

　　2.在方案I的基础上，按压缩费用从少到多的顺序压缩关键线路

　　(1)计算各关键工作的压缩费用

　　关键工作A、B、E、G、L每压缩一天的费用分别为1.5、0.5、0. 25,0.75.1O(万元)o

　　(2)先对压缩费用小于工期奖的工作压缩，即压缩工作E 2d，但工作E压缩后仍不满足合同工期要求，故仍需进一步压缩;再压缩工作B 4d，则工期为268(274 -2 -4=268)d，相应的综合费用为：

　　C’’ =212.5+0.25 ×2 +0.5 ×4 +(268-271)×0.5 =213.5(万元)

　　因此，应在方案I的基础上压缩关键线路来组织施工，相应的工期为268d，相应的综合费用为213.5万元。