名义利率与有效利率
在复利计算中,利率周期通常以年为单位,它可以与计息周期相同,也可以不同。当计息周期小于一年时,就出现了名义利率和有效率的概念。
名义利率i名义是指计息周期利率i乘以一年内的计息周期数m所得的年利率,即:
I名义=i×m
若按月计息,计息期利率为1%,则年名义利率为12%。很显然,计算名义利率时忽略了前面各期利息再生利息的因素,这与单利的计算相同。
有效年利率是指年初的一笔资金按期利率进行计算的年末总利息与年初本金之比。
借款利率,如果借贷资金不是按年结息,应将名义年利率换算为有效年利率。计算公式为:
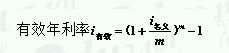
式中 m——每年计息次数。
比较名义年利率为6%的年、半年、季、月的有效年利率。
解: 计息期与有效年利率的关系表
|
名义年利率 |
计息期 |
年计息次数 |
计息期利率 |
有效年利率 |
|
6% |
年 |
1 |
6.0% |
6.0% |
|
半年 |
2 |
3.0% |
6.09% | |
|
季 |
4 |
1.5% |
6.14% | |
|
月 |
12 |
0.5% |
6.17% |
名义利率与实际利率
实际利率是指物价不变,从而货币购买力不变条件下的利率。例如某年度物价没有变化,某甲从某乙处取得1年期的1万元贷款,年利息额500元,则实际利率就是5%。
但是物价不变这种情况在现实经济生活中很少见,如果通货膨胀率为3%,某乙年末收回的1万元本金实际上仅相当于年初的9709元,即10000x100/103=9709元,本金损失率近3%。为了避免通货膨胀给本金带来的损失,假设仍然要取得5%的利息,那么粗略地计算,乙必须把贷款利率提高到8%。这样,才能保证收回的本金和利息之和与以前的相当。这个8%的利率就是名义利率。
因此,名义利率是指包括补偿通货膨胀风险的利率。概略的计算公式可以写成:
i名义=i+p
式中:i名义——名义利率;
i——实际利率;
P——借贷期内通货膨胀率。
但是通货膨胀对于利息部分也有使其贬值的影响。考虑到这一点,名义利率还应有一定的向上调整。
计算题:方圆公司得到一笔100万元贷款,贷款合同规定的年利率为6%,每季度计息一次,贷款期限为3年,到期一次还本付息,计算方圆公司三年期后应支付的利息是多少?
解:先计算有效年利率

第一年产生的利息为:
100×6.14%=6.14(万元)
第二年产生的利息:
(100+6.14)×6.14%=6.52(万元)
第三年产生的利息:
(100+6.14+6.52)×6.14%=6.92(万元)
三年期后方圆公司应支付的利息总和为:6.14+6.52+6.92=19.58(万元)
选择题:已知某项目贷款1000万元,名义利率为6%,每季度计息一次,则项目贷款的有效年利率是( )。
A.6.00%
B.6.09%
C.6.14%
D.6.17%
【答案】C
【解析】名义利率i名义,是指计息周期利率i乘以一年内的计息周期数m所得的年利率;有效年利率是指年初的一笔资金按期利率进行计算的年末总利息与年初本金之比。如果借贷资金不是按年结息,应将名义年利率换算为有效年利率。计算公式为:
有效年利率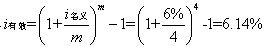 。
。
- ·2019年投资建设项目管理《投资建设项目实施》考试题库我要购买
- ·2019年投资建设项目管理《投资建设项目组织》考试题库我要购买
- ·2019年投资建设项目管理《投资建设项目决策》考试题库我要购买
- ·2019年投资建设项目管理《宏观经济政策》考试题库我要购买
- 12018-02-07我国在世界上具有明显优势的矿产资源包括()
- 22017-08-11比较重要的产业分类主要有()。
- 32017-08-11市场经济的特征有()。
编辑推荐
- 考试题库
- 模拟试题
- 历年真题
