2018年中级审计师考试《财务管理》章节讲解:货币时间价值

第二节　货币时间价值

　　一、货币时间价值的基本原理

　　(一)复利终值与现值

　　1.概念解析：

　　(1)终值(将来值)：现在一定量现金在未来某一时点上的价值，俗称本利和，通常记作F。

　　(2)现值(本金)：指未来某一时点上的一定量资金折合到现在的价值，通常记作P。

　　(3)计息方式：复利计息(利滚利)和单利计息(只就本金计息)

　　2.复利终值：本金与复利计息后的本利和。

　　【推导】

　　FV1=PV+PV×i=PV(1+i)1

　　FV2=PV(1+i)+PV(1+i)×i=PV(1+i)2

　　……

　　FVn=PV(1+i)n=PV·FVIFi,n

　　其中，FVIFi,n为(1+i)n

　　【例1-1】某企业将50 000元存入银行，年利率为5%。该笔存款在5年后的复利终值为?

　　正确答案: FV5=50 000×(1+5%)5≈63 814(元)

　　为便于计算复利终值，可利用复利终值系数表(FVIF表)。查找复利终值系数后计算复利终值如下：50 000×FVIF5%,5 =50 000×1.276=63 800(元)

　　2.复利现值：指未来货币按复利计算的现在价值，即相当于未来本利和的现在价值。

　　【推导】

　　FV1 =PV(1+i)1 → PV=FV1/(1+i)1

　　FV2=PV(1+i)2 → PV=FV2/(1+i)2

　　……

　　FVn=PV(1+i)n → PV=FVn/(1+i)n

　　PV=FVn(1+i)-n= FVn·PVIFi,n，其中PVIFi,n为1/(1+i)n

　　【结论】复利终值系数与复利现值系数之间互为倒数。

　　【例1-2】某企业计划4年后需要150 000元用于研发，当银行存款年利率为5%时，按复利计息，则现在应存入银行的本金为?

　　正确答案:

　　PV=150 000×PVIF5%，4=150 000×0.823=123 450(元)

　　【例题】某投资者希望在2年后支取24 200 元，假如存款年利率为10%，且按复利计息，则现在应存入银行的金额是(　)。

　　A.20 000元　　　B.20 167元

　　C.22 000元　　　D.24 200元

　　正确答案A

　　【例题】某企业将60 000元存入银行，年利率为4%，该笔存款2年后的复利终值是(　)。

　　A.62 400　　　B.62 424

　　C.64 800　　　D.64 896

　　正确答案 C

　　答案解析 60000*(1+4%)2

　　(二)后付年金

　　【分析】年金：一定时期内等额、定期的系列收支。两个特点：一是金额相等;二是时间间隔相等。包括后付年金、先付年金、延期年金、永久年金。

　　【例题】假定政府发行一种没有到期日、不需还本且按年支付固定利息的公债，则该债券利息属于(　)。

　　A.先付年金　　　B.后付年金

　　C.延期年金　　　D.永久年金

　　正确答案 D

　　【例题】某企业决定在未来5年内，每年年初支付300万元的仓储事故保险费。这种年金的类型是(　)。

　　A.先付年金　　　　B.后付年金

　　C.延期年金　　　　D.永续年金

　　正确答案 A

　　答案解析 先付年金是指一定时期内每期期初等额收付款项的年金

　　1.后付年金终值：一定时期内每期期末等额收付款项的复利终值之和。

　　FVAn = A+A(1+i)+A(1+i)2 ……+A(1+i)n-1

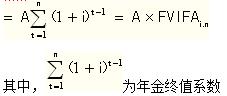
　　【例1-3】某企业在年初计划未来5年每年底将50 000元存入银行，存款年利率为5%，则第5年底该年金的终值为?

　　正确答案 FVA5=50 000×FVIFA5%，5=50000×5.526=276 300(元)

　　2.后付年金现值：一定时期内每期期末等额收付款项的复利现值之和。

　　PVAn = A(1+i)-1+A(1+i)-2 +……A(1+i)-n

　　【例1-4】某企业年初存入银行一笔款项，计划用于未来5年每年底发放职工养老金80 000元，若年利率为6%，问现在应存款多少?

　　正确答案』PVA5=80 000×PVIFA6%,5=80000×4.212=336 960(元)

　　【例题】已知5年期、利率为12%的普通年金终值系数和现值系数分别为6.353和3.605。某企业按12%的年利率取得银行贷款200 000元，银行要求在5年内每年末等额偿付本息，则每年偿付金额应为(　)。

　　A.64 000元　　　　B.554 79元

　　C.40 000元　　　　D.31 481元

　　正确答案B

　　答案解析PVAn=A×PVIFAi，n，所以A=200000/3.605≈55 479

　　(三)先付年金

　　1.先付年金终值的计算

　　(1)计算方法一：Vn=A·(FVIFAi，n+1 -1)

　　【推导】假设最后一期期末有一个等额款项的收付，这样就转换为后付年金的终值问题，由于起点为-1，则期数为n+1，此时F=A·FVIFAi，n+1。然后，把多算的在终值点位置上的A减掉，Vn=A·FVIFAi，n+1-A=A(FVIFAi，n+1-1)

　　(2)计算方法二：先付年金终值=后付年金终值×(1+i)，即 Vn=A·FVIFAi，n·(1+i)

　　A·FVIFAi，n × (1+i)

　　即：(先)预付年金=后付年金×(1+i)

　　【推导】若向前延长一期，起点为-1，则可看出由(-1～n-1)刚好是n个期间，套用后付年金终值的计算公式，得出来的是在第n-1期期末的数值A·FVIFAi，n，为了得出n年末的终值，F=A·FVIFAi，n(1+i)

　　【例1-5】某企业计划建立一项偿债基金，以便在5年后以其本利和一次性偿还一笔长期借款。该企业从现在起每年初存入银行50 209元,银行存款年利率为6%。试问：这项偿债基金到第5年末的终值是多少?

　　正确答案』V5=50 209× FVIFA6%,5×(1+6%)=50209×5.637×1.06≈300 000(元)

　　或V5=50 209×(FVIFA6%，6 -1)=50 209×(6.975-1)≈300 000(元

　　【例题】某企业计划建立一项偿债基金，以便在5年后以其本利和一次性偿还一笔长期借款。该企业从现在起每年年初存入银行30 000元，银行存款年利率为5%(FVIFA5%，5=5.526)。该项偿债基金第5年末的终值是(　)。

　　A.57 000元　　　　　B.150 000元

　　C.165 780元　　　　 D.174 069元

　　正确答案D

　　答案解析30 000×5.526×(1+5%)=174 069元

　　2.先付年金现值的计算

　　(1)计算方法一：V0=A·(PVIFAi，n-1 +1)

　　【推导】假设第1期期初没有等额的收付，这样就转换为后付年金的现值问题，此时期数为n-1，此时P=A* PVIFAi，n-1。然后，把原来未算的第1期期初的A加上，V0=A*PVIFAi，n-1 +A=A(PVIFAi，n-1+1)

　　(2)计算方法二：先付年金现值=后付年金现值×(1+i)，即V0=A·PVIFAi，n·(1+i)

　　A·PVIFAi,n

　　即：先付年金现值=后付年金现值×(1+i)×(1+i)

　　【推导】若向前延长一期，起点为-1，则可看出由(-1～n-1)刚好是n个期间，套用后付年金现值的计算公式，得出来的是在第-1期期末的数值A·PVIFAi，n，为了得出第0点的数值，V0=A·PVIFAi，n·(1+i)

　　【例1-6】某企业租用一台设备,按照租赁合同约定，在5年中每年初需要支付租金6 000元，折现率为7%。问这些租金的现值为多少?

　　正确答案』V0 =6 000×PVIFA7%,5×(1+7%)

　　=6 000×4.100×1.07=26 322(元)

　　或V0 =6 000×(PVIFA7%,4+1)

　　=6 000×(3.387+1)=26 322(元)。

　　【结论】

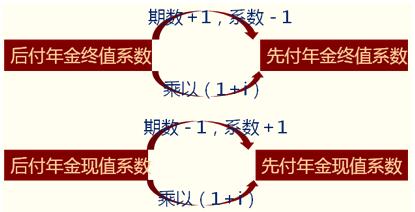
　　(四)延期年金

　　延期年金指的是前几期没有年金，后几期才有年金。

　　设前m期没有年金，后n期才有年金，则该年金构成延期m期的n期延期年金。

　　【例题·单选题】某一项年金前3年没有流入，后第4年开始每年年初流入4000元，则该项年金的递延期是(　)年。

　　A.1　　　　B.2

　　C.3　　　　D.4

　　正确答案』B

　　答案解析前3年没有流入,后4年指的是从第4年开始的,第4年年初相当于第3年年末,这项年金相当于是从第3年末开始流入的,所以,递延期为2

　　1.延期年金终值计算：计算递延年金终值和计算后付年金终值类似。FVAn=A× FVIFAi，n

　　【注意】递延年金终值与递延期无关。

　　2.延期年金现值的计算

　　(1)计算方法一：两次折现法

　　V0=A× PVIFAi,n × PVIFi,m

　　【两次折现推导过程】把递延期以后的年金套用后付年金公式求现值，这时求出来的现值是第一个等额收付前一期期末的数值，距离延期年金的现值点还有m期，再向前按照复利现值公式折现m期即可

　　(2)计算方法二：年金现值系数之差法

　　公式：V0=A×(PVIFAi,n+m - PVIFAi,m)

　　【年金现值系数之差法推导过程】把递延期每期期末都当作有等额的收付A， 把递延期和以后各期看成是一个后付年金，计算出这个后付年金的现值，再把递延期多算的年金现值减掉即可

　　【例1-7】某企业向银行申请取得一笔长期借款，期限为10年，年利率为9%。按借款合同规定，企业在第6-10年每年末偿付本息1 186 474元。问这笔长期借款的现值是多少?

　　正确答案』V0=1186 474×PVIFA9%,5×PVIF9%,5=1186 474×3.890×0.650≈3 000 000(元)

　　或V0=1186 747×(PVIFA9%,5+5-PVIFA9%，5)=1186 747×(6.418-3.890)≈3 000 000(元)

　　(五)永久年金

　　永久年金是指无限期收付款项的年金。

　　1.永久年金没有终值

　　2.永久年金现值=A/i

　　【例1-8】某种永久年金每年收款1 200元，折现率为10%，则该永久年金的现值近似地计算为?

      正确答案V0=1 200× =12 000(元)

　　二、货币时间价值的复杂情况

　　【例1-11】某种年金和不等额系列现金流量混合情况如下表所示，年利率和折现率均为7%：

　　某种年金和不等额系列现金流量混合分布表

　　正确答案

　　(1)终值计算

　　3 000×FVIFA7%,3×FVIF7%,3+4 000×FVIF7%,2+5 000 ×FVIF7%,1+6 000=3 000×3.125×1.225+4000×1.145+ 5 000×1.070+6 000≈27 414(元)

　　(2)现值计算

　　3 000×PVIFA7%,3+4 000×PVIF7%，4+5 000×PVIF7%，5+6 000×PVIF7%，6=3 000×2. 624+4 000 ×0.763+5 000×0.713+6 000×0.666=18 485 (元)

　　三、货币时间价值的特殊情况

　　(一)复利计息频数的影响

　　【推导】1年复利m次，则有m个计息期，每个计息期利率=(名义利率r/m)

　　实际利息=本金×(1+r/m)m-本金

　　=本金×{(1+r/m)m-1}

　　实际利率 i=(1+r/m)m-1

　　1.当m=1时，实际利率=名义利率

　　2.当m>1时，实际利率>名义利率

　　【注意】一年中计息次数越多，复利终值越大;一年中折现次数越多，复利现值越小。

　　【例1-12】假设年初存入银行1 000元，年利率12%。试分别计算按年、半年、季、月计息到年末的复利终值。

　　正确答案

　　按年计息的复利终值=1000×(1+12%)=1120.00(元)

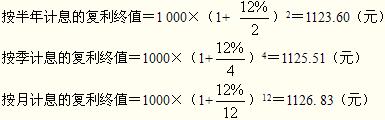
　　【例1-13】假设欲在第三年末获得存款本利和2 000元，年利率12%，试问：若按年、半年、季、月复利折现，第一年初该存款的复利现值即本金各为多少?

　　【例题】某银行推出一种理财产品，年投资收益率为6%。如果半年计息一次，则该理财产品的实际年投资收益率为(　)。

　　A.6%　　　　　 B.6.03%

　　C.6.09%　　　　D.12%

　　正确答案 C

　　(二)折现率和折现期的计算

　　在资金时间价值的计算公式中，都有四个变量(终值或现值、年金、期间、折现率)，已知其中的三个值，就可以推算出第四个的值。前面讨论的是终值FV、现值PV以及年金A的计算。

　　这里讨论的是已知终值或现值、年金、期间，求折现率(之后讲解插值法);或者已知终值或现值、年金、折现率，求期间。

　　【例1-15】某人为购买住房，准备向银行借款300000元,每年偿还借款(含利息)的能力为30 000元，假定年利率5%，按年复利计息，年末还款。其还款期限大约多久?

　　正确答案』根据后付年金现值的计算公式PVAn= A×PVIFAi，n，有PVIFAi,n= PVAn/A，接此例：

　　PVIFA5%，n=300000/30000=10

　　查年金现值系数表：在i=5%时,系数9.899对应的年数n=14，系数10.380对应的年数n=15，由此可知还款期限大约是14～15年。