2022年考研数学一章节习题：函数

　　1、f(x)是二阶常系数非齐次线性微分方程y″+py′+qy=sin2x+2ex的满足初始条件f(0)=f′(0)=0的特解,则当x→0时,

　　A 不存在

　　B 等于0

　　C 等于1

　　D 其他

　　正确答案：C  

　　答案解析：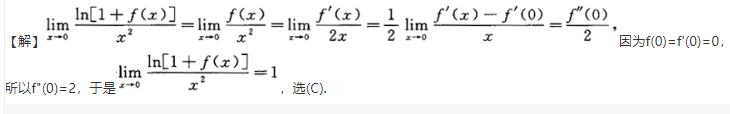

　　2、

　　A A

　　B B

　　C C

　　D D

　　正确答案：B  

　　答案解析：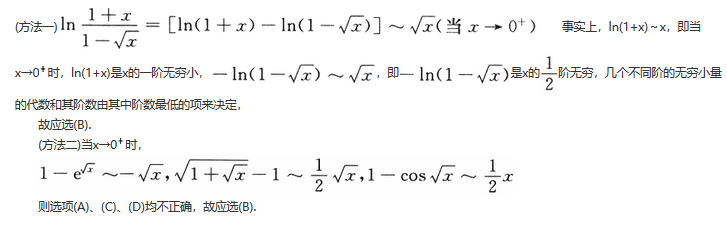

　　3、函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是

　　A 若{xn}收敛，则{f(xn)}收敛

　　B 若{xn}单调，则{f(nx)}收敛

　　C 若{f(xn)}收敛，则{xn}收敛

　　D 若{f(xn)}单调，则{xn}收敛

　　正确答案：B  

　　答案解析：(方法一)由于{xn}单调，f(xn)单调有界，则数列{f(xn)}单调有界.由单调有界准则知数列{f(xn)}收敛，故应选(B).　　(方法二)排除法：若取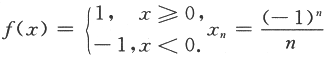，则显然f(xn)单调，{xn}收敛，但显然{f(xn)}不收敛，这样就排除了(A).若取f(xn)=arctanx，x=n，则f(xn)=arctann，显然{f(xn)}收敛且单调，但{xn}不收敛，这样就排除了(C)和(D)，故应选(B).

　　4、“对任意给定的ε∈(0，1)，总存在正整数N，当n>N时，恒有|xn-a|≤2ε”是数列{xn}收敛于a的

　　A 充分条件但非必要条件

　　B 必要条件但非充分条件

　　C 充分必要条件

　　D 既非充分条件又非必要条件

　　正确答案：C  

　　答案解析：本题主要考查考生对数列极限的ε-N定义的理解.其定义是“对任意给定的ε>0，总存在正整数N，当n>N时，恒有|xn-a|<ε”显然，若|xn-a|<ε，则必有|xn-a|≤2ε，但反之也成立，这是由于ε的任意性，对于任意给定的ε1>0，取|xn-a|≤2ε中的，则有即，对任意给定的正数ε1>0，总存在正整数N，当n>N时，恒有|xn-a|<ε1，故应选(C).　　【评注】到目前为止，考研试卷中还没考过利用极限定义证明，或的试题，但从本题可看出，要求考生理解极限的定义.

　　5、已知当x→0时，f(x)=3sinx-sin3x与cx是等价无穷小，则

　　A k=1，c=4

　　B k=1,c=-4

　　C k=3，c=4

　　D k=3,c=-4

　　正确答案：C  

　　答案解析：

　　6、函数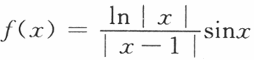，则f(x)有

　　A 1个可去间断点，1个跳跃间断点

　　B 1个可去间断点，1个无穷间断点

　　C 2个跳跃间断点

　　D 2个无穷间断点

　　正确答案：A  

　　答案解析：

　　☛☛☛进入2022年研究生考试练习题库>>>更多考研试题(每日一练、模拟试卷、历年真题、易错题)等你来做!