
[单选题]设函数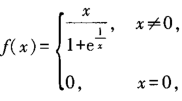 则f(x)在x=0处的左、右导数()。
则f(x)在x=0处的左、右导数()。
A.都存在且相等
B.都不存在
C.都存在但不相等
D.仅有一个存在
参考答案:C
[单选题]设函数f(x)=ax-blnx(a>0)有2个零点,则![]() 的取值范围()。
的取值范围()。
A.(e,+∞)
B.(0,e)
C.(0,![]() )
)
D.(![]() ,+∞)
,+∞)
参考答案:A
由于AB=O,故r(A)+r(B)≤3,又由a,b,c不全为零,可知r(A)≥1。
当k≠9时,r(B)=2,于是r(A)=1;
当k=9时,r(B)=1,于是r(A)=1或r(A)=2。
对于k≠9,由AB=O可得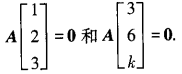
由于η1=(1,2,3)T,η2=(3,6,k)T线性无关。故η1,η2为Ax=0的一个基础解系,于是Ax=0的通解为
x=c1η1+c2η2,其中c1,c2为任意常数。
对于k=9,分别就r(A)=2和r(A)=1进行讨论。
如果r(A)=2,则Ax=0的基础解系由一个向量构成。又因为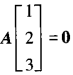 ,所以Ax=0的通解为x=c3(1,2,3)T,其中c3为任意常数。
,所以Ax=0的通解为x=c3(1,2,3)T,其中c3为任意常数。
如果r(A)=1,则Ax=0的基础解系由两个线性无关的解向量构成。又因为A的第一行为(a,b,c)且a,b,c不全为零,所以Ax=0等价于ax1+bx2+x3=0,不妨设a≠0,η3=(-b,a,0)T,η4=(-c,0,a)T是Ax=0的两个线性无关的解,故Ax=0的通解为
x=c4η3+c5η4,其中c4,c5为任意常数。
[问答题]设4阶行列式的第2列元素依次为2,m,k,3,第2列元素的余子式依次为1,-1,1,-1,第4列元素的代数余子式依次为3,1,4,2.且行列式的值为1,求m,k。
参考答案:

[问答题]设3阶矩阵4的特征值为λ1=1,λ2=2,λ3=3,对应的特征向量依次为
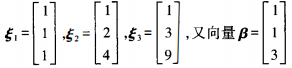
(1)将β用ξ1,ξ2,ξ3线性表出;
(2)求Anβ(n为正整数)。
参考答案:

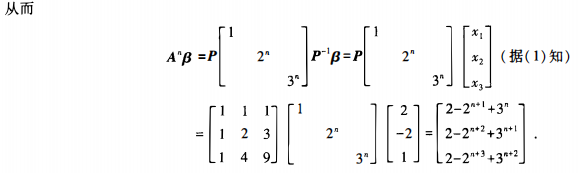
相关文章
报考指南
- 考研真题
- 模拟试题
- 考研备考
