2017教师招聘考试高中物理学科知识-物体平衡相关的弹簧问题

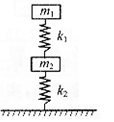
　　例1.如图所示，两木块的质量分别为m1和m2，两轻质弹簧的劲度系数分别为k1和k2，上面木块压在上面的弹簧上(但不拴接)，整个系统处于平衡状态.现缓慢向上提上面的木块，直到它刚离开上面弹簧.在这过程中下面木块移动的距离为( )

　　A.m1g/k1 B.m2g/k2 C.m1g/k2 D.m2g/k2

　　【解题思路】题目问的是下面木块移动的距离，所以解题时抓住下面物块变化前后弹簧的长度进行运算即可。

　　开始时，设弹簧压缩的长度x2，则有m1g+m2g=k2x2

　　得到

　　当上面的木块刚离开上面弹簧时，设弹簧压缩的长度x2′，则有

　　m2g=k2x2′得到

　　所以在这过程中下面木块移动的距离为h=x2-x2′= m1g/k2，所以选C

　　命题要点二：突变问题

　　在弹簧两端都保持与其他物体接触的条件下，弹簧弹力的大小F=kx与形变量x成正比，由于形变量的改变需要一定时间，因此这种情况下，弹力的大小不会突然改变。(这一点与绳不同，高中物理研究中，绳的形变很微小可以忽略不计，因此绳两端所受弹力可以突变。)

　　例2.如图所示，质量为m的小球用水平弹簧连接，并用倾角为30°的光滑木板AB托住，使小球恰好处于静止状态。当AB 突然向下撤离的瞬间，小球的加速度为 ( )

　　A.0

　　B.大小为g，方向竖直向下

　　C.大小为 ，方向垂直于木板向下

　　D. 大小为 , 方向水平向右

　　【解题思路】木板撤去前，小球处于平衡态，受重力、支持力和弹簧的拉力，如图

　　当AB 突然向下撤离的瞬间， FN突然消失，因为重力大小方向都不变，弹簧弹力不会发生突变，所以撤离瞬间小球受到的重力、弹簧的拉力跟撤去前是一样的，因此此时所受的合力应该与之前的FN等大反向。

　　命题要点三：临界问题

　　两个相互接触的物体被弹簧弹开，这两个物体在什么位置恰好分开?这属于临界问题。“恰好分开”既可以认为已经分开，也可以认为还未分开。认为已分开，那么这两个物体间的弹力必然为零;认为未分开，那么这两个物体的速度、加速度必然相等。同时利用这两个结论，就能分析出当时弹簧所处的状态 。

　　临界时特点：1.接触;2.具有共同的加速度;3.相互之间的弹力减小为0

　　例3. 如图所示，两个木块A、B叠放在一起，B与轻弹簧相连，弹簧下端固定在水平面上，用竖直向下的力F压A，使弹簧压缩量足够大后，停止压缩，系统保持静止。这时，若突然撤去压力F，A、B将被弹出且分离。下列判断正确的是( )

　　A.木块A、B分离时，弹簧的长度恰等于原长

　　B.木块A.B分离时，弹簧处于压缩状态，弹力大小等于B的重力

　　C.木块A、B分离时，弹簧处于压缩状态，弹力大小等于A、B的总重力

　　D.木块A、B分离时，弹簧的长度可能大于原长

　　【解题思路】抓住分离瞬间的特点去分析。A、B分离时，二者之间无挤压，因此A的加速度为g，对于B，分离瞬间二者加速度应该相等，所以B的加速度也为g，因此此时B不受弹簧弹力的作用，弹簧处于原长，选A。

　　结论：仅靠弹簧弹力将两物体弹出，那么这两个物体必然是在弹簧原长时分开的。

　　例4.如图所示，质量均为m的A、B两物体叠放在竖直弹簧上并保持静止，用大小等于mg的恒力F向上拉B，运动距离h时，B与A分离，下列说法正确的是( )

　　A.B和A刚分离时，弹簧长度等于原长

　　B.B和A刚分离时，它们的加速度是g

　　C.弹簧的劲度系数等于mg/h

　　D.在B和A分离前，它们做匀加速直线运动

　　【解题思路】AB分离条件：AB间没有弹力作用，且具有相同的加速度

　　假设分离时还没有恢复原长，则

　　对A：kx-mg=ma

　　对B：F-mg=ma

　　又因为F=mg

　　联立上式有：kx=mg，x≠0，所以不是原长时分离，分离时a=0，AB错;

　　A、B两物体叠放在竖直弹簧上并保持静止时，弹力大小为2mg，分离时为mg，即弹力变化量为mg，故弹簧的劲度系数等于mg/h，C对;

　　在B与A分离之前，F-2mg+F弹=ma，弹力逐渐减小，加速度逐渐增大，它们作加速度逐渐减小的加速运动，D错。

　　结论：除了弹簧弹力，还有其它外力作用而使相互接触的两物体分离。那么两个物体分离时弹簧必然不一定是原长。