2017教师招聘考试学科知识数学试题二

　　数学专业基础知识

　　一、选择题(在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的代悟填入题后括号内。本大题共7小题，每小题2分，共14分。)

　　1、下列图形中，是中心对称图形但不是轴对称图形的是(　　).

　　2、若a，b∈R，i为虚数单位，且(a+i)i=b+i，则(　　).

　　A.a=1，b=1

　　B.a=-1，b=1

　　C.a=-1，b=-1

　　D.a=1，b=-1

3、

　　A.x>2

　　B.x≥2

　　C.x≠2

　　D.x≤2

　　4、长方体的主视图、俯视图如下图所示(单位：m)，则其左视图面积是(　　).

　　A.4m2

　　B.12 m2

　　C.1 m2

　　D.3 m2

5、 A. B. C. D.

　　6、若函数f(x)=lg(ax2-4x+a-3)的值域为R，则实数口的取值范围是(　　).

　　A.(4，+∞)

　　B.[0，4]

　　C.(0，4)

　　D.(-∞，-1)∪(4，+∞)

7、

　　A.P(k)对k=2004成立

　　B.P(k)对每一个自然数k成立

　　C.P(k)对每一个正偶数k成立

　　D.P(k)对某些偶数可能不成立

　　二、填空题(本大题共6小题，每空2分，共12分。)

8、

　　9、 已知关于x的方程3x-2m=4的解是x=m，则m的值是_________.

10、

　　11、 某射手射击所得环数ξ的分布列如下：

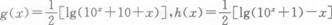
　　已知ξ的期望Eξ=8.9，则y的值为_________.

　　12、 已知点E、F分别在正方体ABCD—A1B1C1D1的棱BB1、CC1上，且B1E=2EB1CF=2FC1，则面AEF与面ABC所成的二面角的正切值等于__________.

13、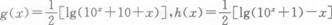

　　三、计算题(本大题共2小题，每小题7分，共14分)

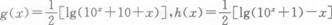
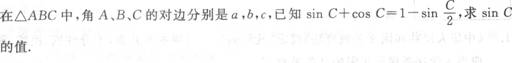
14、 15、

　　四、应用题(10分)

　　16、如下图1是一个三棱柱包装盒，它的底面是边长为10cm的正三角形，三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2)，然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分)，纸带在侧面缠绕三圈，正好将这个三棱柱包装盒的侧面全部包贴满.

　　(1)请在图2中，计算裁剪的角度∠BAD;

　　(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.

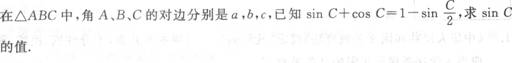
　　五、证明题(本大题共2小题，每小题10分，共20分)

　　17、在平行四边形ABCD中，∠DAB=60°，AB=15cm.已知⊙O的半径等于3cm，AB，AD分别与⊙O相切于点E，F，⊙O在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止，试求⊙O滚过的路程.

　　18、 为了进一步了解某校九年级学生的身体素质情况，体育老师对该校九年级(1)班50位学生进行了一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，图表如下所示：

　　请结合图表完成下列问题：

　　(1)求表中a的值;

　　(2)若在一分钟内跳绳次数少于120次的为测试不合格，则该校九年级(1)班学生进行一分钟跳绳不合格的概率是多少?

　　第二部分 教育理论与实践

　　一、单项选择题(在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的代号填入题后括号内。本大题共5小题，每小题1分，去5分。)

　　19、 如右图所示，菱形ABCD中，点E是CD边上一点，连接AE，交对角线BD于点F，连接CF，则图中全等三角形共有(　　)对.

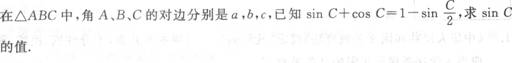
　　A.1

　　B.2

　　C.3

　　D.4

　　20、 把一个平行四边形沿一条直线对折，且使折痕把这个平行四边形的面积两等分，符合要求的折叠方法(　　).

　　A.没有

　　B.有2种

　　C.有4种

　　D.有无数种

21、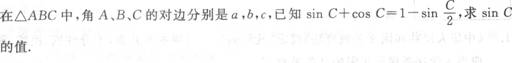

　　A.圆x2+y2=2内

　　B.圆x2+y2=2上

　　C.圆x2+y2=2外

　　D.以上三种情况都有可能

　　22、 当今教育改革的核心是(　　).

　　A.教学方法改革

　　B.课程改革

　　C.教育评价制度改革

　　D.教育结构改革

　　23、学校教育的基础是(　　).

　　A.教师

　　B.学生

　　C.班级

　　D.课程

　　二、多项选择题(在每小题的五个备选答案中，选出二至五个正确的答案，并将正确答案的序号分别填在题干的括号内，多选、少选、错选均不得分。本大题共2小题，每小题2.5分，共5分。)

　　24、我国义务教育的学制通常有(　　).

　　A.“六三”学制

　　B.“五四”学制

　　C.“九年一贯制”

　　D.“四二”学制

　　25、 教师的教育能力是指(　　).

　　A.人际关系处理能力

　　B.课前准备能力

　　C.语言表达能力

　　D.班级管理能力

　　三、填空题(本大题共3小题，每空1分，共10分)

　　26、教学是学校的________工作，是贯彻国家的教育方针，实现教育目的的________.

　　27、师生关系在人格上是_________的关系，在社会道德上是_________的关系.

　　28、 教学过程的基本要素为_______、_______、_______.

　　四、简答题(10分)

　　29、什么是解题方法多样化?解题方法的多样化有什么作用?如何促进解决问题方法的多样化?