2018年监理工程师考试《投资控制》章节讲义：第三章第一节

2018年监理工程师考试《投资控制》章节讲义：第三章第一节

第三章　建设工程设计阶段的投资控制

第一节　资金时间价值

　　一、现金流量

　　1.现金流量的概念

　　◇三个：现金流入量CI(流入经济系统或方案的资金);现金流出量CO(流出经济系统或方案的…);净现金流量NCF或(CI-CO)t(同一时点上的现金流入量与现金流出量之差)。

　　2.现金流量图

　　◆现金流量的三要素：现金流量的大小;方向(流入或流出);作用点(发生时间-某计算期的期末)。

　　3.现金流量表

　　二、资金时间价值的计算

　　(一)资金时间价值的概念

　　◆含义：资金因参与流通，随着时间的延伸而产生增值(利润或利息)的现象或属性。

　　◇实质(增值-利息)：资金提供者，补偿;资金使用者，代价。

　　(二)资金时间价值计算的种类

　　◇三个：等值(等效值);未来值(终值);现在值(现值)。

　　(三)利息和利率

　　◇本金、利息与利率

　　1.单利法

　　◇利不生利：

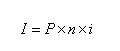
　　(式3-2)

　　◇例3-1P39

　　2.复利法

　　◆利上加利：

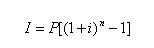
　　(式3-5)

　　◆在单利、复利两种计息方法中，如果未做特殊说明，应当选择(默认)复利法(计息)。

　　(四)实际利率和名义利率

　　【补例1】某人向您借款10万元，借期2年，每个季度计息一次，季度利率是2%。则到期后的利息应为多少?

　　【解】该例题，有以下不同算法，并引发实际利率和名义利率的区别：

　　第一种算法：100000×(1+2%×4×2)=116000元，利息为16000元;

　　第二种算法：100000×(1+2%×4)2=116640元，利息为16640元;

　　年度利率·复利计息

　　第三种算法：100000×(1+2%)4×2=117165.94元，利息为17165.94元。

　　季度利率·复利计息

　　◇题中的利息的差异，主要源于1年内的各个计息周期(季度)之间是否复利计息。其中，第一种算法中的年利率8%，属于名义利率;第三种算法中的年利率(1+2%)4-1=17.17%，属于实际利率。

　　1.名义利率

　　◇含义：计息周期利率乘以每年计息的周期数。例如，上例中的8%，其各个季度之间属于单利计息。

　　2.实际利率(有效利率)P40

　　◆如果年名义利率为r、一年内的计息周期次数为m，则年实际利率(i)可按下式计算：

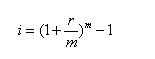
　　(式3-8)

　　对于补例而言，年实际利率为17.17%。

　　【例3-3】某公司存入银行10万元，年利率为2.79%，共存5年，按复利每半年计息1次，问存款到期后利息?P40

　　【解】已知P=10，r=2.79%，m=2，n=5

　　①按年实际利率计算：由i=(1+2.79%/2)2-1=2.81%，则F=10×(1+2.81%)5=11.486(万元)。

　　②按计息周期利率计算：2.79%/2→n=10(个半年);

　　F=10×(1+2.79%/2)10=11.486(万元)。

　　◆于是，利息=11.486-10=1.486(万元)。

　　3.实际利率的讨论

　　①当m=1时，实际利率(i)等于名义利率(r);

　　②当m>1(计息周期不足1年)时，实际利率(i)将大于名义利率(r)，而且m越大，二者相差也越大;

　　③m<1，只有数学意义，没有经济意义。

　　◆一年内的各个计息周期之间采用单利计息，属于名义利率;各个计息周期之间是复利计息，则为实际利率。而且，未来应该选择实际利率(式3-8)。

　　(五)资金时间价值计算的基本概念和符号

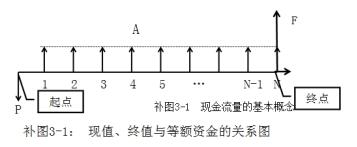
　　1.现值(P)：资金发生在(或折算为)某一时间序列起点时间的价值，或相对于将来值的任何较早时间的价值;

　　2.终值(F)将来值、本利和

　　：资金发生在(或折算为)某一时间序列终点时间的价值，或相对于现在值的任何较晚时间的价值;

　　3.等额年金或等额资金(A)：发生在或折算为某一时间序列各个计算期期末(不包括零期)的等额资金的价值。参见教材P41图3-2，或补充的图3-1。

　　(六)复利法资金时间价值计算的基本公式

　　1.一次支付的终值公式(已知P，i、n，求F)P41：图3-3

　　◆在一次支付的背景下，已知计息周期利率i，则n个计息周期(年)末的终值(本利和)F，可下式计算：

　　F=P(1+i)n(式3-9)

　　◆其中，(1+i)n为一次支付的终值系数，记为(F/P，i，n)或理解为(F←P，i，n)。它可以描述用途或功能(做什么)，并在有关数据已知的情况下，得出数值(做到什么程度)。

　　2.一次支付的现值公式(已知F，i、n，求P)

　　◆由终值公式(3-9)的逆运算，可得现值P的计算式为：P=F(1+i)-n(式3-10)

　　◆其中，(1+i)-n为现值系数，记为(P/F，i，n)。

　　【例3-4】某公司计划2年以后购买100万元的…，。

　　【解】已知F=100万元，n=2年，i=2.25%

　　则P=F(1+i)-n=100×(1+2.25%)-2=95.648(万元)

　　◆将不同时间的资金进行折现或称贴现，更加常用。

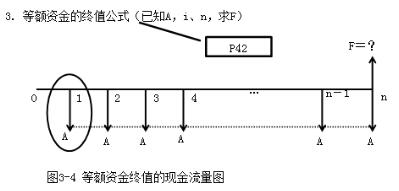
　　◆其计算(推导)式为：

　　F=A(1+i)n-1+A(1+i)n-2+…+A=

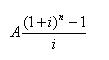
　　(式3-11) ◆在式3-11中，

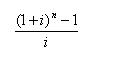
　　称为年金终值系数，记为(F/A，i，n)。

　　【例3-5】…，每月月末存入200元，月利率为1.43‰，求年底积累的储蓄额?

　　【解】由式3-11，则F=200×12.0948=2418.96(元)

　　◇形象记忆：已知年轻时每年等额存入一笔钱(存款、养老保险)，则到一定年龄后，可以一次性地取出多少钱?

　　4.等额资金偿债基金公式(已知F，i、n，求A)

　　◆由等额资金终值公式(3-11)的逆运算，可得偿债基金公式为：

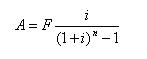
　　(式3-12) ◆其中，

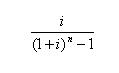
　　称为偿债基金系数，记为(A/F，i，n)。

　　◇形象记忆：为了未来N年后一次性支取的定额养老金，现在开始应等额存入的款项;图3-5。P42

　　5.等额资金的回收公式(已知P，i、n，求A)

　　◆由“P→F”(式3-9)和“F→A”(式3-11)，可有等额资金回收公式(参见图3-6)：

　　等额资金回收系数(式3-13)

　　【例3-7】P=100万元，i=10%，n=5。则A=?

　　由式3-13及已知条件，则A=26.38万元

　　◇形象记忆：在住房按揭贷款中，已知贷款额，求一定期限内的月供或年供。

　　6.等额资金的现值公式(已知A，i、n，求P)

　　◆由等额资金回收公式(式3-13)的逆运算，可得等额资金的现值公式：

　　(式3-14) ◆其中

　　，称为年金现值系数，记为(P/A，i，n)。

　　【例3-8】A=100万元，i=5.76%，n=6年。P=?

　　由式3-14及已知条件，则P=495.46(万元)

　　◇形象记忆：先存后取的养老金模式(以后若干年内，每年领取年金若干，求当初存入多少钱)。

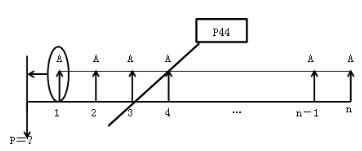
　　图3-7等额资金现金流量图

　　◆注意：P与首个A，只能间隔一个计息周期。

　　监理工程师培训辅导—2018年监理工程师VIP套餐

　　适应人群：首次报考或者基础薄弱的学员，确保两年内获取证书的学员

　　包含课程：精讲班+冲刺班+习题班;赠送真题班+六科全真模拟考场+评测后导师点评+考试不过2019年免费重学

　　详细情况：报名VIP套餐学习，赠送真题班+全真摸底评测+评测后导师点评;

　　● 报名VIP套餐学习，考试不过2019年免费重学;

　　● 报名VIP含教材套餐，新教材出版后安排派送;

　　全国统一服务热线：4000-525-585　快速联系通道